<<返回       
                              §7 向量到子空间的最小距离·最小二乘法

在解析几何中，两个点和间的距离等于向量的长度.

一.   向量的距离

1.定义13 长度称为向量和的距离，记为

2.距离的性质：

1）;2），并且仅当时等号才成立；

3）（三角不等式）

二.向量与子空间的最小距离

在中学所学几何中知道一个点到一个平面（一条直线）上所有点的距离以垂线最短.下面可以证明一个固定向量和一个子空间中各向量间的距离也是以“垂线最短”.

1.              设子空间W是由向量所生成，即.说一个向量垂直于子空间W，就是指向量垂直于W中任何一个向量.

2.垂直于W的充要条件是垂直于每个.

3.结论:给定，设y是W中的向量，满足垂直于W.则对于W中任一向量，有.

我们可以画出下面的示意图：

证明 因W是子空间，,则.故垂直于.由勾股定理，故.这就证明了，向量到子空间各向量间的距离以垂线最短.

这个几何事实可以用来解决一些实际问题.其中的一个应用就是解决最小二乘法问题.

三 最小二乘法问题：

1．引例 已知某种材料在生产过程中的废品率y与某种化学成分x有关.下列表中记载了某工厂生产中y与相应的x的几次数值：

我们想找出y对x的一个近似公式.

2．线性方程组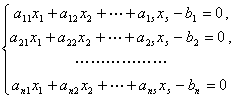可能无解.即任何一组数都可能使

                  (1)

不等于零.我们设法找 使（1）最小，这样的 称为方程组的最小二乘解.这种问题就叫最小二乘法问题.

2.最小二乘解所满足的代数条件

令

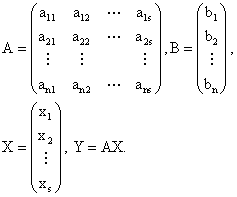             (2)

用距离的概念，（1）就是

最小二乘法就是找使Y与B的距离最短.但从（2），知道向量Y就是

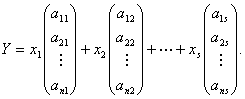
把A的各列向量分别记成.由它们生成的子空间为.Y就是 中的向量.于是最小二乘法问题可叙述成：

找X使（1）最小，就是在中找一向量Y，使得B到它的距离比到子空间中其它向量的距离都短.

应用前面所讲的结论，设是所求的向量，则.必须垂直于子空间.为此只须而且必须

回忆矩阵乘法规则，上述一串等式可以写成矩阵相乘的式子，即

而按行正好排成矩阵，上述一串等式合起来就是

或

附：证明：必有解。

证明：分两步：（1）证明：的秩= A的秩

(2)……

结论：就是最小二乘解所满足的代数方程，它是一个线性方程组，系数矩阵是，常数项是..

引例的解答，易知              

最小二乘解a,b所满足的方程就是,

即为解得（取三位有效数字）.

      瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）