§6 实对称矩阵的标准形   <<返回

由第五章得到，任意一个对称矩阵都合同于一个对角矩阵，换句话说，都有一个可逆矩阵C使成对角形.现在利用欧氏空间的理论，第五章中关于实对称矩阵的结果可以加强.

一．实对称阵：元素为实数的对称阵。

问题：实对称阵能否通过相似变换成为标准形。

注：上学期已经知道，：实对称阵能通过合同变换成为标准形。但合同变换与相似变换不同。

二．实对称阵的特性

1．引理1 设A是实对称矩阵，则A的特征值皆为实数.

证明：设出A的任一特征值与相应的特征向量，然后设出对应的共轭的特征值与特征向量.

    考察。利用实对称阵的特点，得。最后证明即可。

2．实对称阵与线性变换的对应：A为实数域R上的n 级方阵。在n维欧氏空间上定义一个线性变换A如下：

A.                         (1)

显然A在标准正交基

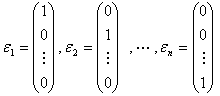                  (2)

下的矩阵就是A.

3．引理2 设A是实对称矩阵，A的定义如上，则对任意，有

(A,)=(,A),                      (3)

或

注意：可以写成二种形式：与.

证明：只要证明后一等式即可：

4．引理3 设A是实对称矩阵，则中属于A的不同特征值的特征向量必正交.

证明：利用引理2的结论和方法……

三．对称变换

1．定义12 欧氏空间中满足等式(3)的线性变换称为对称变换.

2．结论：对称变换在标准正交基下的矩阵是实对称矩阵.反之，实对称阵A也对应对称变换A.

3．引理4 设A是对称变换，是A-子空间，则也是A-子空间.

证明：根据概念与引理2的结论……

四．实对称阵的对角形

1．定理7 对于任意一个n级实对称矩阵A，都存在一个n级正交矩阵T，使成为对角形.

证明：只要证明对称变换A有n个特征向量做成标准正交基。

   对空间的维数n用数学归纳法。

   第2步：设n-1时定理成立。对n维欧氏空间，线性变换A有一特征向量，其特征值为实数。将单位化，还用代表。作的正交补。此正交补是不变子空间且维数为n-1此时可用归纳假设……

注：相似变换对应的阵“T”（）中的列向量组即为特征向量作成的标准正交基，因此  可视为  的过渡阵。

2．正交矩阵T的求法步骤

分析：在定理的证明中看到，矩阵A按(1)式在中定义了一个线性变换.求正交矩阵T的问题就相当于在中求一组由A的特征向量构成的标准正交基.事实上，设

是的一组标准正交基，它们都是A的特征向量.显然，由到的过渡矩阵就是

T是一个正交矩阵，而就是对角形.

步骤：

（1）. 求出A的特征值.设是A的全部不同的特征值.

（2）. 对于每个，解齐次方程组

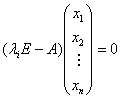
求出一个基础解系，这就是A的特征子空间的一组基.由这组基出发，按定理2的方法求出的一组标准正交基.

（3）. 因为两两不同，所以根据这一节引理4，向量组还是两两正交的.又根据定理7以及第七章§5的讨论，它们的个数就等于空间的维数.因此，它们就构成的一组标准正交基，并且也都是A的特征向量.这样，正交矩阵T也就求出了.

例 已知

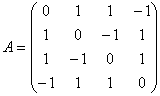
求一正交矩阵T使成对角形.

解：特征值：1（三重），-3. 正交阵：

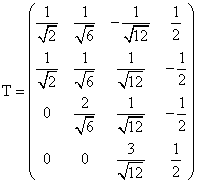    。标准型。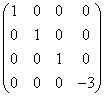

注：1.在定理7中，对于正交矩阵T我们还可以进一步要求

事实上，如果求得的正交矩阵T的行列式为-1，那么取

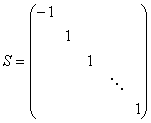
那么是正交矩阵，而且显然.

2．如果线性替换

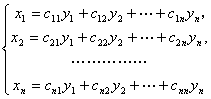
的矩阵是正交的，那么它就称为正交的线性替换.正交的线性替换当然是非退化的.

五.正交变换化二次型为标准形

1．定理8 任意一个实二次型

都可以经过正交的线性替换变成平方和,其中平方项的系数就是矩阵A的特征多项式全部的根.

       这是定理7用二次形的描述

六.正交变换化二次型为标准型

1．定理8 任意一个实二次型都可以经过正交的线性替换变成平方和,其中平方项的系数就是矩阵A的特征多项式全部的根.

    2．几何意义：化简直角坐标系下二次曲线的方程

在直角坐标系下，二次曲线的一般方程是

  (5)

令              

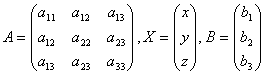
则(5)可以写成                                 (6)

经过转轴，坐标变换公式为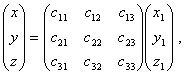或者

其中C为正交变换且，在新坐标系中，曲面的方程就是

根据上面的结果，有行列式为1的正交矩阵C使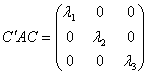

这就是说，可以作一个转轴，使曲面在新坐标系中的方程为

其中.这时，再按照是否为零的情况，作适当的移轴与转轴就可以把曲面的方程化成标准方程.譬如说，当全不为零时，就作移轴

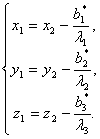
于是曲面的方程化为.其中 .

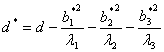      瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）