§2  正交基      <<返回

一、标准正交基

1．定义5 欧氏空间V的一组非零的向量,如果它们两两正交，就称为一个正交向量组.

注：按定义，由单个非零向量所成的向量组也是正交向量组.

2．结论：正交向量组是线性无关的.这说明，n维欧氏空间中两两正交的非零向量不能超过n个.

3．定义6 在n维欧氏空间中，由n个向量组成的正交向量组称为正交基；由单位向量组成的正交基称为标准正交基组.

对一组正交基进行单位化就得到一组标准正交基.

二、标准正交基的判断与存在性

1．欧氏空间一组基为标准正交基的充要条件：它的度量矩阵为单位矩阵.

设是一组标准正交基，由定义，有

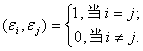                                   (1)

所以此基的度量矩阵为单位矩阵.反之亦显然

2．在n维欧氏空间中，标准正交基是存在的.

因为度量矩阵是正定矩阵，根据第五章关于正定二次型的结果，正定矩阵合同于单位矩阵.这说明在n维欧氏空间中存在一组基，它的度量矩阵是单位矩阵.

3．标准正交基下向量坐标与内积的表示

（1）向量表示：.                   (2)

（2）内积表示：设

那么                      (3)

这个表达式正是几何中向量的内积在直角坐标系中坐标表达式的推广.

应该指出，内积的表达式(3)，对于任一组标准正交基都是一样的.这说明了，所有的标准正交基，在欧氏空间中有相同的地位.

三、正交化方法

1．定理1 n维欧氏空间中任一个正交向量组都能扩充成一组标准正交基.

证明：对n-m用数学归纳法：在第二步中找出不能被表示出的向量后做正交化……

注：定理的证明实际上也就给出了一个具体的扩充正交向量组的方法…

2．定理2 对于n维欧氏空间中任意一组基，都可以找到一组标准正交基，使

证明：逐个地求，类似定理1的方法……

注：1)应该指出，定理中的要求

就相当于由基到基的过渡矩阵是上三角形的.

2)定理2 中把一组线性无关的向量变成一单位正交向量组的方法在一些书和文献中称为施密特（Schimidt）正交化过程.

例1 变成单位正交组.

(,,

)

四、正交矩阵

1．一组标准正交基到另一组标准正交基的过渡阵.

设与是欧氏空间V中的两组标准正交基，它们之间的过渡矩阵是，即

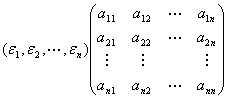
因为是标准正交基，所以

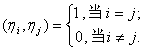                              (4)

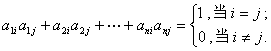矩阵A的各列就是在标准正交基下的坐标.按公式(3),(4)式可以表示为                   (5)

(5)式相当于一个矩阵的等式                         (6)

或者

2．定义7 n组实数矩阵A称为正交矩阵，如果

3．结论：由标准正交基到标准正交基的过渡矩阵是正交矩阵；反过来，如果第一组基是标准正交基，同时过渡矩阵是正交矩阵，那么第二组基一定也是标准正交基.

注：根据逆矩阵的性质，由即得.写出来就是

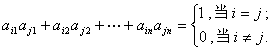                 (7)

(5)式是矩阵列与列之间的关系，(7)式是矩阵行与行之间的关系.这两组关系是等价的.

例2  判断矩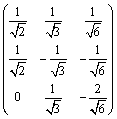阵 是否正交阵

例3 欧氏空间的基

,

是 的一个标准正交基.

     瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）