§1定义与基本性质 <<返回
一、向量的内积
定义1
设V是实数域R上一个向量空间,在V上定义了一个二元实函数,称为内积,记作![]() ,它具有以下性质:
,它具有以下性质:
1)
![]() ;
2)
;
2) ![]() ;
;
3)
![]() ;
4)
;
4) ![]() ,当且仅当
,当且仅当![]() 时,
时,
![]()
这里![]() 是V任意的向量,k是任意实数,这样的线性空间V称为欧几里得空间.
是V任意的向量,k是任意实数,这样的线性空间V称为欧几里得空间.
例1
在线性空间![]() 中,对于向量
中,对于向量![]() ,
,
定义内积![]() (1)
(1)
则内积(1)适合定义中的条件,这样![]() 成为一个欧几里得空间.仍用
成为一个欧几里得空间.仍用![]() 表示.
表示.
在![]() 时,(1)式就是几何空间中的向量的内积在直角坐标系中的坐标表达式.
时,(1)式就是几何空间中的向量的内积在直角坐标系中的坐标表达式.
例2
在![]() 里,
对于向量
里,
对于向量![]() ,定义内积
,定义内积
![]()
则内积(1)适合定义中的条件,这样![]() 就也成为一个欧几里得空间.仍用
就也成为一个欧几里得空间.仍用![]() 来表示它
来表示它
注:对同一个线性空间可以引入不同的内积,使得它作成欧几里得空间.
例3
在闭区间![]() 上的所有实连续函数所成的空间
上的所有实连续函数所成的空间![]() 中,对于函数
中,对于函数![]() 定义内积
定义内积![]() .
(2)
.
(2)
对于内积(2),![]() 构成一个欧几里得空间.
构成一个欧几里得空间.
同样地,线性空间![]() 对于内积(2)也构成欧几里得空间.
对于内积(2)也构成欧几里得空间.
二、欧几里得空间的基本性质
1)定义中条件1)表明内积是对称的.
![]() .
.
![]()
三.向量的长度与夹角
(一)长度
1.定义2
非负实数![]() 称为向量
称为向量![]() 的长度,记为
的长度,记为![]() .
.
显然,向量的长度一般是正数,只有零向量的长度才是零,这样定义的长度符合熟知的性质:
![]() (3)
(3)
这里![]() .
.
长度为1的向量叫做单位向量.如果,![]() 由(3)式,向量
由(3)式,向量![]() 就是一个单位向量.用向量
就是一个单位向量.用向量![]() 的长度去除向量
的长度去除向量![]() ,得到一个与
,得到一个与![]() 成比例的单位向量,通常称为把
成比例的单位向量,通常称为把![]() 单位化.
单位化.
2.柯西-布涅柯夫斯基不等式:即对于任意的向量![]() 有
有
![]() (5)
(5)
当且仅当![]() 线性相关时,等式才成立.
线性相关时,等式才成立.
证明:![]() =0时显然,下设
=0时显然,下设![]() 。
。
令![]() (t为实变量)由此得
(t为实变量)由此得![]() 。展开后取
。展开后取![]() 即可证明出所需结论……
即可证明出所需结论……
例:对于例1的空间![]() ,(5)式就是
,(5)式就是
![]()
对于例2的空间![]() ,(5)式就是
,(5)式就是
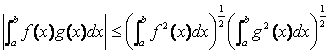
(二)夹角
1.定义3
非零向量![]() 的夹角
的夹角![]() 规定为
规定为
![]()
![]() .(根据柯西-布涅柯夫斯基不等式)
.(根据柯西-布涅柯夫斯基不等式)
3.定义4
如果向量![]() 的内积为零,即
的内积为零,即![]()
那么![]() 称为正交或互相垂直,记为
称为正交或互相垂直,记为![]() .
.
注:(1)两个非零向量正交的充要条件是它们的夹角为![]() .
.
(2)只有零向量才与自己正交.
4.勾股定理:当![]() 正交时,
正交时,![]()
推广:如果向量两![]() 两两正交,那么
两两正交,那么
![]() .
.
四.度量矩阵
1.设V是一个n维欧几里得空间,在V中取一组基![]() ,令
,令![]() (8)
(8)
矩阵![]() 称为基
称为基![]() 的度量矩阵
的度量矩阵
2.度量矩阵的作用:度量矩阵完全确定了内积.
设V,![]() 同上,对于V中任意两个向量
同上,对于V中任意两个向量
![]() ,
,![]() ,
,
由内积的性质得
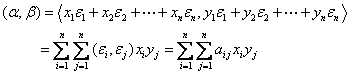
显然![]() 于是
于是![]() (9)
(9)
利用矩阵,![]() 还可以写成
还可以写成![]() ,
(10)
,
(10)
其中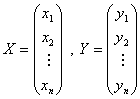 分别是
分别是![]() 的坐标,而.上面的讨论表明,在知道了一组基的度量矩阵之后,任意两个向量的内积就可以通过坐标按(9)或(10)来计算。
的坐标,而.上面的讨论表明,在知道了一组基的度量矩阵之后,任意两个向量的内积就可以通过坐标按(9)或(10)来计算。
3.不同基的度量矩阵的关系
设![]() 是空间V的另外一组基,而由
是空间V的另外一组基,而由![]() 到
到![]() 的过渡矩阵为C,即
的过渡矩阵为C,即![]() 于是不难算出,基
于是不难算出,基![]() 的度量矩阵
的度量矩阵
![]() .
(11)
.
(11)
这就是说,不同基的度量矩阵是合同的.(书中习题11)
4.度量矩阵与正定矩阵的关系
根据条件(4),对于非零向量![]() ,即
,即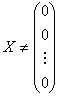 有
有![]() 因此,度量矩阵是正定的.
因此,度量矩阵是正定的.
反之,给定一个n级正定矩阵A及n维实线性空间V的一组基![]() .可以规定V上内积,使它成为欧几里得空间,并且基的
.可以规定V上内积,使它成为欧几里得空间,并且基的![]() 度量矩阵是A.
度量矩阵是A.
5.欧几里得空间的子空间在所定义的内积之下也是一个欧几里得空间.
欧几里得空间以下简称为欧氏空间.
例:在 中(内积按通常定义)求与向量 和 均正交的向量的全体。它们能否构成 的子空间?求它的基与维数。
瀚海代数精品课程网资源 (需要原word文档请联系:nchy_zouzij@163.com)