§7 矩阵的有理标准形   <<返回

前一节中证明了复数域上任一矩阵A可相似于一个若尔当形矩阵.这一节将对任意数域P来讨论类似的问题.我们证明了P上任一矩阵必相似于一个有理标准形矩阵.

一、有理标准型的概念

1、定义8 对数域P上的一个多项式。称矩阵

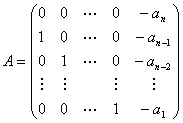                        (1)

为多项式 的伴侣阵.

注：容易证明，A的不变因子(即的不变因子)是

.（见习题3）

2、定义9 下列准对角矩阵

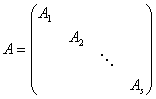,                      (2)

其中 分别是数域P上某些多项式 的伴侣阵，且满足 ，A就称为P上的一个有理标准形矩阵.

注：有理标准形与若当标准形均为准对角形。

二、矩阵化有理标准型

1、引理 (2)中矩阵A的不变因子为，其中1的个数等于的次数之和n减去s.

证明：根据

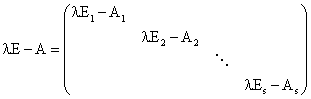
再根据上面“注”中的结论，可将每一块 通过初等变换变成

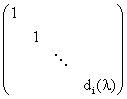
进而将整个矩阵变成需要证明的形式……

2、 定理14 数域P上 方阵A在上相似于唯一的一个有理标准形，称为A的有理标准形.

证明：先设A的（的）不变因子为1,1,…,1,…。设出的伴侣阵，并将它们构成一个准对角阵B.比较A与B的不变因子……

把定理14的结论变成线性变换形式的结论就成为

3、定理15 设A是数域P上n维线性空间V的线性变换，则在V中存在一组基，使A在该基下的矩阵是有理标准形，并且这个有理标准形由A唯一决定的，称为A的有理标准形.

例1 设矩阵A的初等因子为，则它的不变因子是1，，它的有理标准形为

..

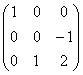   例2 

    瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）