§5  初等因子   <<返回

一、初等因子的概念

1．定义7 把矩阵A（或线性变换A）的每个次数大于零的不变因子分解成互不相同的一次因式方幂的乘积，所有这些一次因式方幂(0次不算，相同的必须按出现的次数计算)称为矩阵A (或线性变换A)的初等因子.

例 设12级矩阵的不变因子是

.

按定义，它的初等因子有7个，即

.

其中出现三次，出现二次.

2．不变因子和初等因子的关系.

  （1）初等因子在不变因子列的位置。

首先，假设n级矩阵A的不变因子为已知.将分解成互不相同的一次因式方幂的乘积：

,

,

,

                （思考：为什么不是？）

则其中对应于的那些方幂就是A的全部初等因子.注意不变因子有如下性质，即

,

从而          .

因此在的分解式中，属于同一个一次因式的方幂的指数有递升的性质，即           .

这说明，同一个一次因式的方幂作成的初等因子中，方次最高的必定出现在的分解中，方次次高的必定出现在的分解中.如此顺推下去，可知属于同一个一次因式的方幂的初等因子在不变因子的分解式中出现的位置是唯一确定的.

（2）．从初等因子和矩阵的级数唯一地作出不变因子的方法.

设一个n级矩阵的全部初等因子为已知，在全部初等因子中将同一个一次因式的方幂的那些初等因子按降幂排列，而且当这些初等因子的个数不足n时，就在后面补上适当个数的1，使得凑成n个.设所得排列为

.

于是令           ,

则就是A的不变因子.

（3）．定理8 两个同级复数矩阵相似的充要条件是它们有相同的初等因子.

证明：上面作不变因子的方法说明：如果两个同级的数字矩阵有相同的初等因子，则它们就有相同的不变因子，因而它们相似.反之，如果两个矩阵相似，则它们有相同的不变因子，因而它们有相同的初等因子。

二、初等因子的求法

初等因子和不变因子都是矩阵的相似不变量.但是初等因子的求法与不变因子的求法比较，反而方便一些.

引理1如果多项式都与互素，则.

.

证明：证明等式两边可以相互整除：先证明右边整除左边，右边为两个数的乘积，显然两数各自都整除左边，余下的问题就是证明右边两式互素（据即证）

    再证明左边整除右边：左边是公因式，则必为的因式，将此因式分解成的因式与的因式的乘积。最后证明这两个因式分别整除右边的两个因式……

引理2 设               ,

,

如果多项式都与互素，则和等价.

证明：就看它们有没有相同的行列式因子。证明它们有相同的一级行列式因子时需要用引理1……

定理9 首先用初等变换化特征矩阵为对角形式，然后将主对角线上的元素分解成互不相同的一次因式方幂的乘积，则所有这些一次因式的方幂(相同的按出现的次数计算)就是A的全部初等因子.

证明：将对角形设出后，需要证明的就是：对于每个相同的一此因式的方幂在的主对角线上按递升幂次排列后，得到的新对角阵与等价。此时就是的标准形而且所有不为1的就是A的全部初等因子。

      据引理，每一对初等因子可以对调。这样，只要对每一类初等因子用引理2，就可以实现要求的目的。。。。。

例： 若等价于

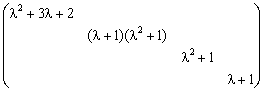
求 的标准形。

解：初等因子：

  标准形：

三．现在可以总结一下判断矩阵A 的若当标准形A的形式的步骤：

1．  由上一章第8节，必存在。

2．  由第8章第4节，A，相似

3．  由第8章第1，3，5节，A与有相同的初等因子。

4．  由第8章第5节，讨论不必求不变因子求初等因子的方法。

5．  由第8章第6节（下一节），求出若当块及若当型阵的初等因子。问题解决。

      瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）