§4 矩阵相似的条件     <<返回

在求一个数字矩阵A的特征值和特征向量时曾出现过矩阵,我们称它A为的特征矩阵.这一节的主要结论是证明两个数字矩阵A和B相似的充要条件是它们的特征矩阵和等价.

引理1 如果有数字矩阵使,                (1)

当且仅当A和B相似.

证明：将等式展开再比较两边即可得到结论。

引理2 对于任何不为零的数字矩阵A和矩阵与，一定存在矩阵与以及数字矩阵和使

,               (2)

.               (3)

证明：把改写成多项式的形式：

然后类似数字多项式的“带余除法”….

定理7 设A，B是数域P上两个矩阵. A与B相似的充要条件是它们的特征矩阵和等价.

证明：先证明必要性：设A与B相似，即有可逆矩阵T，使

于是，从而两者等价。

再证明充分性：设与等价，即有可逆的矩阵与使

成立。用引理2的式子代入…，整理后得：

右端次数等于1或，因此是数字矩阵，记作T,立即有：

下面只需要证明T可逆：由上面第一式得：

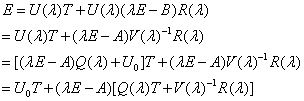
等式右端的第二项必须为零……

注：矩阵A的特征矩阵的不变因子以后简称为A的不变因子.

因为两个矩阵等价的充要条件是它们有相同的不变因子，所以由定理7即得

推论 矩阵A与B相似的充要条件是它们有相同的不变因子.

应该指出，矩阵的特征矩阵的秩一定是n.因此，矩阵的不变因子总是有n个，并且，它们的乘积就等于这个矩阵的特征多项式.

以上结果说明，不变因子是矩阵的相似不变量，因此我们可以把一个线性变换的任一矩阵的不变因子(它们与该矩阵的选取无关)定义为此线性变换的不变因子.

瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）