§2 矩阵在初等变换下的标准形   <<返回

一．矩阵的初等变换与初等矩阵

1．定义3 下面的三种变换叫做矩阵的初等变换：

(1) 矩阵的两行（列）互换位置；

(2) 矩阵的某一行（列）乘以非零的常数c；

(3) 矩阵有某一行（列）加另一行（列）的倍，是一个多项式.

2． 矩阵的初等矩阵.例如，将单位矩阵的第j行的 倍加到第i行上得

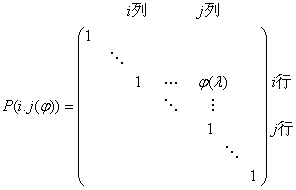
仍用P(i,j)表示由单位矩阵经过第i行第j行互换位置所得的初等矩阵，用P(i(c))表示用非零常数c乘单位矩阵第i行所得的初等矩阵.同样地，对一个 的 矩阵 作一次初等变换就相当于在 的左边乘上相应 的初等矩阵；对 作一次初等列变换就相当于 在的右边乘上相应的 的初等矩阵.

3．初等矩阵都是可逆的，并且有

.

由此得出初等变换具有可逆性……

二．矩阵的的等价

1．定义4 矩阵称为与等价，如果可经一系列初等变换将化为.

2．等价是矩阵之间的一种关系，这个关系的性质：

(1) 反身性……(2) 对称性……(3) 传递性……

应用初等变换与初等矩阵的关系即得，矩阵与等价的充要条件为有一系列初等矩阵，使.               (2)

3．矩阵可以经过初等变换化为某种对角矩阵.

引理 设矩阵的左上角元素，并且中至少有一个元素不能被它除尽，那么一定可以找到一个与等价的矩阵，它的左上角元素也不为零，但是次数比的次数低.

证明：根据中不能被除尽的位置，分三种情况：

    1）的第一列中有一个元素不能被除尽，则用对作带余除法，然后据带余除法对第i列做行变换……

     2) 的第一行中有一个元素不能被除尽，类1）的证明，作列变换……

    3) 1)与2）均不满足，但不能被除尽，先作行列对换后成为前面的 情形。

定理2 任意一个非零的的矩阵都等价于下列形式的矩阵

,

其中 是首项系数为1的多项式，且

.

这个矩阵称为的标准形.

证明：运用引理，先作若干线性变换，使得第一行第一列上的元素可以除尽其余的所有元素，然后用初等行列变换将第一行与第一列中除外均成为0.对其余行列继续下列作法…..

例 用初等变换化矩阵

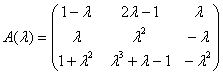
为标准形.

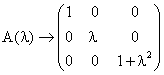
      瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）