§9 最小多项式    <<返回

这一节讨论应用最小多项式来判断一个矩阵能否对角化的问题.

一．矩阵的最小多项式

1．根据哈密尔顿—凯莱定理，任给数域P上一个级矩阵A，总可以找到数域P上一个多项式f(x)，使f(A)=0.如果多项式f(x)使f(A)=0，就称f(x)以A为根.以A为根的多项式中次数最低的首项系数为1的以A为根的多项式称为A的最小多项式.

2．以A为根的多项式必存在，从而最小多项式亦存在.

3．四个引理

1）引理1 矩阵A的最小多项式是唯一的。

证明：用常规的方法：假设有两个最小多项式，将它们分别用带余除法，最后证明它们相等…

2）引理2 设g(x)是矩阵A的最小多项式，则f(x)以A为根的充要条件是g(x)\f(x) .

证明：完全用同引理1的方法可以证明。（给同学们做练习）

    推论：矩阵A的特征多项式必为A的最小多项式的倍式。

由此可知，矩阵A的最小多项式是A的特征多项式的一个因式.

例1 数量矩阵kE的最小多项式为x-k，零矩阵的最小多项式为x.另一方面，如果A的最小多项式是1次多项式，那么A一定是数量矩阵.

例2 设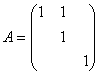求A的最小多项式.

（先求A 的特征多项式，可见特征多项式是最小多项式的倍式……..其最小多项式为

）

例3 设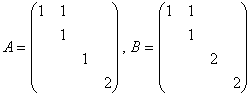.A与B的最小多项式都等于，但是它们的特征多项式不同，因此A和B不是相似的.

3）引理3 设A是一个准对角矩阵

,

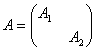并设的最小多项式为，的最小多项式为,那么A的最小多项式为,的最小公倍式.

证明：记,由

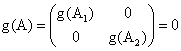
因此g(x)是A的最小多项式的倍式;

     要证明g(x)最小，可令h(A)=0，那么

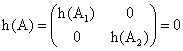
所以，因而，即……

推论：如果

,

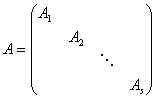的最小多项式为，那么A的最小多项式为

4）引理4 k级若尔当块

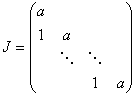
的最小多项式为.

证明：只要证明（i=1,…k-1）,而（据J的特征多项式为）.

    3．最小多项式与矩阵对角化

定理15 数域P上n级矩阵A与对角矩阵相似的充要条件为A的最小多项式是P上互素的一次因式的乘积.

证明：根据引理3的推广，必要性成立。

    充分性：首先据矩阵与线性变换的对应关系，可定义线性变换A的最小多项式等于对应矩阵A的最小多项式。那只需证明：若数域P上某线性空间V上的线性变换A的最小多项式g(x)是P上互素的一次因式的乘积：，则A有一组特征向量做成V 的基.

    由于g(A)V=0.用定理12中同样步骤可证，其中

                          A

把各自的基合起来就是V 的基。而每个基向量都属于某个，因而是A的特征向量。

推论 复数矩阵A与对角矩阵相似的充要条件是A的最小多项式没有重根.

    瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）