§8 若尔当(Jordan)标准形介绍   <<返回

由前面的讨论可知，并不是对于每一个线性变换都有一组基，使它在这组基下的矩阵成为对角形.下面先介绍一下，在适当选择的基下，一般的一个线性变换能化简成什么形状.

一．若尔当矩阵

1．定义8 形式为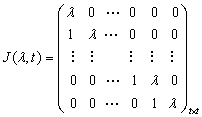的矩阵称为若尔当(Jordan)块，其中是复数.由若干个若尔当块组成的准对角矩阵称为若尔当形矩阵，其一般形状如

                        (1)

其中,（中有一些可以相等）.

例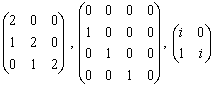 都是若尔当块，而

是一个若尔当形矩阵.

注：（1）一级若尔当块就是一级矩阵，因此若尔当形矩阵中包括对角矩阵.

2．若当标准形。。。。

3．在一个线性变换的若尔当标准形中，主对角线上的元素正是特征多项式的全部的根（重根按重数计算）.（先设若当标准型存在，然后据线性变换后矩阵相似……）

二．矩阵化若尔当标准形

1．定理13 设A是复数域上线性空间V的一个线性变换，则在V中必定存在一组基，使A在这组基下的矩阵是若尔当形矩阵.

证明：由定理12可知V可以分解成一些A的不变子空间的直和。那么问题就变成了在这些不变子空间内找一组基，使得线性变换限制在各子空间内在此基下的矩阵为若当型矩阵。先且看下列引理：

引理 n维线性空间V上的一个线性变换B满足

B=ℴ,是某正整数，就称B为V上幂零线性变换.对幂零线性变换B ，V中必有下列形式的一组元素作为基

                            (2)

于是B在这组基下的矩阵

证明：对维数用归纳法证明：设线性空间维数<n时，引理的结论成立，则维数=n时：

    首先容易证明得到B V的维数<n.将B看成B V上的线性变换，仍有B=ℴ。由归纳假设，B V上有基

由于均属于B V，找出它们在B上的原像再置换。注意置换后的倒数第二行：

是B的核B^-1（0）中的向量，它们是B V的基中的部分向量，故线性无关，要组成B^-1（0）的一组基，必须加一些向量构成B^-1（0）的一组基……

现在回来证明定理13，因为已经证明在上有（A-。作B=（A-，则B

用引理的结论容易得出结论……

上述结果用矩阵表示就是：

2．定理14 每个n级复矩阵A都与一个若尔当形矩阵相似.

注：这里数域P必须为复数域，不然未必有此结论。

  瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）