§7  不变子空间   <<返回

对于给定的n维线性空间V,A∈L(V),如何才能选到V的一个基,使A关于这个基的矩阵具有尽可能简单的形式..这一节介绍不变子空间的概念，来说明线性变换的矩阵的化简与线性变换的内在联系.

一．问题：对于V的一个线性变换。若不能将它适当取基下成为对角形，则能否适当取基使之成为近似的对角形？

二．不变子空间的概念

1．定义7  设A是数域P上线性空间V的线性变换,W是V的一个子空间.如果对于W中任一向量，有A，就称W是A的不变子空间，简称A-子空间.

例1 整个空间V和零子空间{0},对于每个线性变换A，都是A-子空间. A的值域与核都是A-子空间.

例2         （非不变子空间之例）.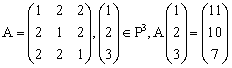

令V=P³,W=,AV=.此时W非A的不变子空间。

例3 若线性变换A与B是可交换的，则B的核与值都是A-子空间.因为A的多项式f(A)是和A交换的，所以f(A)的值域与核都是A-子空间.

例4 任何一个子空间都是数乘变换的不变子空间.

2．A-子空间的和与交还是A-子空间.

3．特征向量与一维不变子空间的联系：一维不变子空间的生成元必为特征向量；反之，特征子空间的任一特征向量生成的子空间为不变子空间。

设W是一维A-子空间，是W中任何一个非零向量，它构成W的一个基.按A-子空间的定义，A,它必是的一个倍数:A.这说明是A的特征向量，而W即是由生成的一维A-子空间.

反过来，设是A属于特征值的一个特征向量，则以及它任一倍数在A下的像是原像的倍，仍旧是的一个倍数.这说明的倍数构成一个一维A-子空间.

显然，A的属于特征值的一个特征子空间也是A的不变子空间.

结论：若能找到n 个线性无关的特征向量 ，记 分别为生成的子空间，则.

3．不变子空间的判断：如果线性空间V的子空间W是由向量组生成的，即，则W是A-子空间的充要条件为A,A,…, A全属于W.

4．设A是线性空间V的线性变换, W是A的不变子空间.把A看成是W的一个线性变换，称为A限制在不变子空间W上引起的变换.用符号A|W来表示（但是在不致引起混淆的情况下，仍然用A来表示）.

注：A与A|W的异同：A是V的线性变换, V中每个向量在A下都有确定的像；A|W是不变子空间W上的线性变换，对于W中任一向量，有(A|)=A.但是对于V中不属于W的向量来说，（A|）是没有意义的.

例 任一线性变换在它的核上引起的变换就是零变换，而在特征子空间上引起的变换是数乘变换.

三．不变子空间与线性变换矩阵化简之间的关系.

1．A在不变子空间W上引起的变换。

2．设A是维线性空间V的线性变换，W是V的A-子空间.在W中取一组基,并且把它扩充成V的一组基

.                        (1)

那么，A在这组基下的矩阵就具有下列形状

.              (2)

并且左上角的k级矩阵 就是A|W在的基 下的矩阵.

2．设V分解成若干个A-子空间的直和：.在每一个A-子空间中取基

                       (3)

并把它们合并起来成为V的一组基I.则在这组基下，A的矩阵具有准对角形状

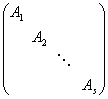                       (4)

其中 就是A|W在基(3)下的矩阵.

反之，如果线性变换A在基I下的矩阵是准对角形（4），则由（3）生成的子空间 是A-子空间.

结论：矩阵分解为准对角形与空间分解为不变子空间的直和是相当的.

四．空间V分解成不变子空间的直和.

定理12 设线性变换A的特征多项式为，它可分解成一次因式的乘积

则V可分解成不变子空间的直和

其中

证明：令以及（A）V.则是A 的值域。由本节的例3知道  是A 的不变子空间。且满足（A A）V=0.

      下面的问题就是证明：。根据概念验证即可。

      验证第一点时要用到。验证第二点设

只要证明每一即可（将（A）作用于上式两边……）

    最后不要忘记证明：。只要证明：的核上的任一点属于。

      瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）