§6 线性变换的值域与核 <<返回
一．定义6
设A是线性空间V的一个线性变换，A的全体像组成的集合称为A的值域，用AV表示.所有零向量关于A的原象组成的向量的集合称为A的核，用A
表示.
AV的维数称为A的秩，A的维数称为A的零度.
注：（1）若用集合的记号则A
=
,A=
（2）线性变换的值域与核都是V的子空间.
例1
在线性空间
中，令D
则D
的值域就是
，D
的核就是子空间
.
二．AV的描述
1．定理10
设A是n维线性空间V的线性变换，
是V的一组基，在这组基下A的矩阵是A，则
1）
A的值域AV是由基像组生成的子空间，即A
=
(注意：A
,A
,…,A
未必线性无关)
2） A的秩=A的秩.
证明：1）将任一值域中的值用
表示出来即可
2）据1），A的秩等于基像组的秩。另外，A的每一列即为基像组的坐标，基像组与坐标组由同构有相同的秩。
注：定理10说明线性变换与矩阵之间的对应关系保持不变.
例
已知
的线性变换
A ((a,b,c))=(a+2b-c,b+c,a+b-2c)
求A的秩与零度。
(A
P3的一组基:
A
(
)=(1,0,1)
A
(
)=(2,1,1)
A-1（0）的基（3，-1，1）)
三.A的秩与零度的关系。
定理11
设A是n维线性空间V的线性变换，则AV的一组基的原像及A的一组基合起来就是V的一组基.由此还有A的秩+A的零度=n.
证明：设出AV的一组基的原像及A的一组基，用常规的方法证明它们合起来是线性无关（统一做线性变换即可）。再证明任一向量可以被此组基线性表示，只要通过此向量在线性变换的像用AV的一组基线性表示，然后返回到V……
推论 对于有限维线性空间的线性变换，它是单射的充要条件是它是满射.
证明：容易看到，当且仅当AV=V时，A是满射；当且仅当A的零度为0时，A为单射。从定理11可见两者等价。
虽然子空间AV与A的维数之和为
，但是AV+A并不一定是整个空间.
例2
设A是一个
矩阵，
.证明A相似于一个对角矩阵
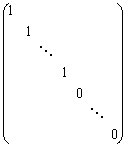
证明：将A看成是某线性变换A在某基下的矩阵，只要证明：在一组适当的基下，A的矩阵为上述矩阵即可。
由A2=A，得A2=A。只要取AV的一组基……再取A-1（0）的一组基……,合起来就是。
瀚海代数精品课程网资源 （需要原word文档请联系：nchy_zouzij@163.com）