§5  对角矩阵   <<返回

一．矩阵化对角形的条件

1．充要条件：定理7 设A是n维线性空间V的一个线性变换，A的矩阵可以在某一基下为对角矩阵的充要条件是A有n个线性无关的特征向量.

证明：必要性据概念，充分性只要将线性无关的特征向量作为基。

2．对角形的具体判别

1）定理8 属于不同特征值的特征向量是线性无关的.

证明：对特征值的个数用数学归纳法：在第二步中利用特征值的特点： A.进行消元……

推论1 如果在n维线性空间V中，线性变换A的特征多项式在数域P中有n个不同的根，即Å有n个不同的特征值，那么A在某组基下的矩阵是对角形的.

推论2 在复数域上的线性空间中，如果线性变换A的特征多项式没有重根，那么A在某组基下的矩阵是对角形的.

证明：因为复数域中任一n次多项式都有n个根。

在一个线性变换没有n个不同的特征值的情形，要判断这个线性变换的矩阵能不能成为对角形，问题就要复杂些.

2）定理9 如果是线性变换A的不同的特征值，而是属于特征值的线性无关的特征向量，那么向量组也线性无关.

证明：类似用定理8的方法，用数学归纳法（给同学们作为练习）

3）判别法：（1）据定理9，对于一个线性变换，求出属于每个特征值的线性无关的特征向量.那么这个线性变换在一组合适的基下的矩阵是对角矩阵当且仅当它们的个数等于空间的维数。并且对角阵上主对角线上的元素除排列次序外是唯一确定的，它们正好是A的特征多项式全部的根（重根按重数计算）.

（2）设A全部不同的特征值是，于是A在某一组基下的矩阵成对角形的充要条件是A的特征子空间的维数之和等于空间的维数.

应该看到，当线性变换A在一组基下的矩阵A是对角形时：

A的特征多项式就是

4．等价的结论：

  若矩阵A 可以化成对角形当且仅当A 有n 个线性无关的特征向量。且对角形中对角线上的元素为A的特征值。相似变换为.

例1：已知3级方阵A 的特征值为1,1,0. 对应的特征向量为

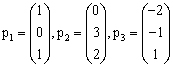
求矩阵A.

                         (A=)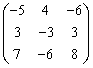

例2 在§4的例2中，已经算出线性变换A的特征值是-1（二重）与5，而对应的特征向量是

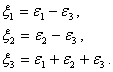
由此可见，A在基下的矩阵为对角矩阵

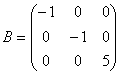
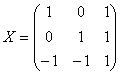而由到的过渡矩阵是于是，

.

     瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）