§4 特征值与特征向量   <<返回

一．      问题

（1）对数域P上的任一n维线性空间V上的线性变换A（对应某基下的矩阵为A ）能否适当的选择V的另一组基, 使A在此基下的矩阵为对角形？

 （2）对任一数域P 上的n阶方阵A是否可以通过相似变换成为对角形？

注：问题（1）与（2）是等价的。

二．初步分析

先设存在矩阵X 使

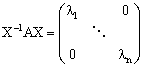
将X写成如下形式

即有。

      说明为矩阵方程的解。。。。

二、线性变换的特征值和特征向量的概念

1．定义4 设A是数域P上线性空间V的一个线性变换,如果对于数域P中一数,存在一个非零向量,使得 A=.                               （1）

那么称为A的一个特征值,而叫做A的属于特征值的一个特征向量.

2．几何意义：特征向量的方向经过线性变换后，保持在同一条直线上，这时或者方向不变或者方向相反,至于时，特征向量就被线性变换变成0.

注：（1）特征向量不是被特征值所唯一决定的.相反，特征值却是被特征向量所唯一决定的。一个特征向量只能属于一个特征值.

（2）在问题2中对角形中对角线上的元素即为特征值。相似变换中对应矩阵的各列向量即特征向量。（存在性尚未证）

三、特征值与特征向量的求法

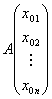1．分析：设V是数域P上n维线性空间，是它的一组基，线性变换A在这组基下的矩阵是A.设是特征值，它的一个特征向量在下的坐标是,则A的坐标是。的坐标是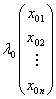

因此（1）式相当于坐标之间的等式 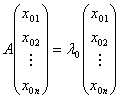                      (2)

或            

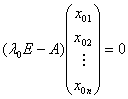
这说明特征向量 的坐标 满足齐次方程组

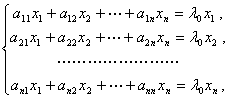
即 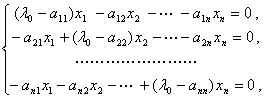                                 (3)

由于,所以它的坐标 不全为零，即齐次方程组有非零解.而齐次方程组有非零解的充要条件是它的系数行列式为零，即

.

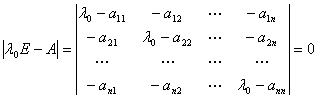（先求特征值，再求特征向量。）

四、1．分析…

2．定义5 设A是数域P上一个n级矩阵,是一个数字.矩阵的行列式

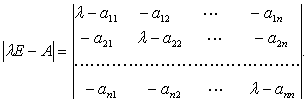                  (4)

叫做矩阵A的特征多项式。

注:从上面说明，特征多项式的根对应所有线性变换A的特征值，这样,将特征值代入上述特征方程就得到特征向量.

3．确定一个线性变换A的一个特征值与特征向量的步骤：

（1）在线性空间V中取一组基，写出A在这组基下的矩阵A；

（2）求出特征多项式在数域P中全部的根，它们也就是线性变换A的全部特征值；

（3）把所求得的特征值逐个地代入方程组（3），对于每一个特征值，解方程组（3），求出一组基础解系，它们就是属于这个特征值的几个线性无关的特征向量在基下的坐标，这样，也就求出了属于每个特征值的全部线性无关的特征向量.

注：矩阵A的特征多项式的根有时也称为A的特征值，而相应的线性方程组（3）的解也就称为A的属于这个特征值的特征向量.

例1 在n维线性空间中，数乘变换K在任意一组基下的矩阵都是kE，它的特征多项式是.

因此，数乘变换K的特征值只有k，由定义，每个非零向量都是属于K的特征向量.

例2 设线性变换A在基下的矩阵是

,

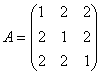求A的特征值与对应的线性无关的特征向量.

（特征值：-1（二重），5；特征向量： ）

例3 在空间中，线性变换D在基下的矩阵是

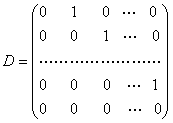
D的特征多项式是     .

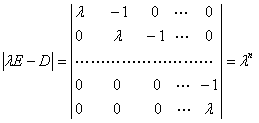因此，D的特征值只有0.通过解相应的齐次线性方程组知道，属于特征值0的线性无关的特征向量组只能是任一非零常数.这表明微商为零的多项式只能是零或非零的常数.

例4 平面上全体向量构成实数域上一个二维线性空间，§1例1中旋转ℱ在直角坐标系下的矩阵为它的特征多项式为

当 时，这个多项式没有实根.因之，当 时，ℱ 没有特征值.从几何上看，这个结论是明显的.

4．对于线性变换A的任一个特征值，全部适合条件A的向量所成的集合，也就是A的属于的全部特征向量再添上零向量所成的集合，是V的一个子空间，称为A的一个特征子空间，记为.

显然，的维数就是属于的线性无关的特征向量的最大个数.用集合记号可写为.

五．矩阵的特征多项式的系数.

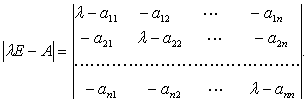
的展开式中，有一项是主对角线上元素的连乘

展开式中的其余项，至多包含n-2个主对角线上的元素，它对的次数最多是n-2.因此特征多项式中含的n次与n-1次的项只能在主对角线上元素的连乘积中出现，它们是

.

在特征多项式中令，即得常数项.

因此，如果只写特征多项式的前两项与常数项，就有

.             (5)

结论：由根与系数的关系可知：1）A的全体特征值的和为（称为A的迹）.2）A的全体特征值的积为.

特征值自然是被线性变换所决定的.但是在有限维空间中，任取一组基后，特征值就是线性变换在这组基下矩阵的特征多项式的根.随着基的不同，线性变换的矩阵一般是不同的.但是这些矩阵是相似的，对于相似矩阵有

六．1．相似阵的特征值的关系

定理6 相似矩阵有相同的特征多项式.

证明：只要证明它们有相同的特征多项式……

注：（1）线性变换的矩阵的特征多项式与基的选取无关，它直接被线性变换所决定的.因此，以后就可以说线性变换的特征多项式了.

（2）这不等于说，有相同的特征多项式必相似！（相似变换未必存在）

既然相似的矩阵有相同的特征多项式，当然特征多项式的各项系数对于相似的矩阵来说都是相同的.考虑特征多项式的常数项，得到相似矩阵有相同的行列式.因此，以后就可以说线性变换的行列式.

注：定理6的逆是不对的，特征多项式相同的矩阵不一定是相似的(未必找得到相似变换).例如

它们的特征多项式都是，但A和B不相似，因为和A相似的矩阵只能是A本身.

   2．结论：（1）相似阵有相同的特征多项式。

     （2）这也说明了矩阵若可以通过相似变换化对角形，则对角形除对角线上元素排列顺序不同外唯一确定。

七．哈密顿-凯莱(Hamilton-Caylay)定理 设A是数域P上一个矩阵，是A的特征多项式，则

问题：能否用（5）代入A的方法？

证明：关键是由行列式的性质，设B()是E-A 的伴随矩阵，有下式：

  上式两边都是矩阵多项式。设出f()的系数，然后比较两边的系数，得：

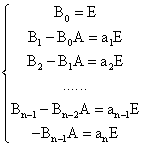
以Aⁿ,A^n-1,…,A,E分别右乘上面各式，再相加，使左边为0，右边则为f(A)……

推论 设A是有限维空间V的线性变换，是A的特征多项式，那么(A)=ℴ.

瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）