§3 线性变换的矩阵 <<返回
一、线性变换与矩阵的对应
1．线性变换通过基唯一确定
预备结论：如果确定了线性变换对基
的像，那么线性空间中任意一个向量
的像也唯一确定。
设是数域P上n维线性空间V的一组基.空间V中任意一个向量可以被基线性表出，即有关系式
(1)
其中系数是唯一确定的，它们就是在这组基下的坐标.由于线性变换保持线性关系不变，因而在的像A与基的像A
,A
,…，A
之间也必然有相同的关系：
A=A（
）=
A()+
A()+…+
A
()
(2)
引理1.
设是线性空间V的一组基，如果线性变换Å与ℬ在这组基上的作用相同，即A
=B，
那么A=
B.
结论1的意义就是，一个线性变换完全被它在一组基上的作用所决定.下面指出，基向量的像却完全可以是任意的，也就是
引理2.
设是线性空间V的一组基，对于任意一组向量
一定有一个线性变换A使A=
证明：关键是作出这样的线性变换。实际上“A=”已给出了答案。最后要证明它是线性变换。
定理1
设是线性空间V的一组基，是V中任意n个向量.存在唯一的线性变换Å使A=
2．定义2
设是数域P上n维线性空间V的一组基，A是V中的一个线性变换.基向量的像可以被基线性表出：
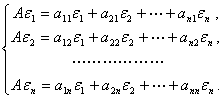
用矩阵表示就是
A（）=（A()，AÅ()，…，
A()）=
(5)
其中
，称为线性变换A在基下的矩阵.
注：A（）=（A()，A()，…，
A()）是一种形式的规定
例1
设
是n(n>m)维线性空间V的子空间W的一组基，把它扩充为V的一组基.指定线性变换A如下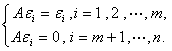
如此确定的线性变换A称为子空间W的一个投影.不难证明A
=A
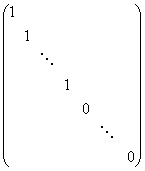
投影A在基下的矩阵是
二、V上线性变换的空间与
的同构
1.预备：在取定一组基之后，就建立了由数域P上的n维线性空间V的线性变换到数域P上的
矩阵的一个双射.前面引理1说明这个映射是单射，引理2说明这个映射是满射.换句话说，在这二者之间建立了一个双射.这个对应的重要性表现在它保持运算，即有
2．定理2
设是数域P上n维线性空间V的一组基，在这组基下，每个线性变换按公式（5）对应一个矩阵，这个对应具有以下性质：
1）线性变换的和对应于矩阵的和；
2）线性变换的乘积对应于矩阵的乘积；
3）线性变换的数量乘积对应于矩阵的数量乘积；
4）可逆的线性变换与可逆矩阵对应，且逆变换对应于逆矩阵.
证明：写出线性变换在基下的矩阵表示即可全部证出。
3．结论：定理2
说明数域P上n维线性空间V的全体线性变换组成的集合L(V)对于线性变换的加法与数量乘法构成P上一个线性空间，与数域P上n级方阵构成的线性空间
同构.
三、线性变换的下的坐标表示
定理3
设线性变换A在基下的矩阵是
，向量在基下的坐标是
,则A在基下的坐标
可以按公式
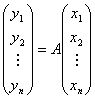
计算.
证明：将任意一个向量用基线性表示（写成矩阵形式）。然后对此式两边作线性变换。最后比较两种坐标表示形式即得。
注：在基变换与坐标变换中，若
与
是V中的二组基。过渡阵为A:
则向量
在
下的坐标
与在
下的坐标
的关系是
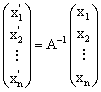
将上式中的
作为线性替换A（满足A
）对应的矩阵，即：
四、同一个线性变换在不同基下的矩阵的关系.
线性变换的矩阵是与空间中一组基联系在一起的.一般说来，随着基的改变，同一个线性变换就有不同的矩阵.为了利用矩阵来研究线性变换，有必要弄清楚线性变换的矩阵是如何随着基的改变而改变的.
定理4设线性空间V中线性变换A在两组基
,
(6)
(7)
下的矩阵分别为A和B从基（6）到（7）的过渡矩阵是X，于是
.
证明：已知
（A
，A
,…,A
）=（,,…,
）A
（A
,A
,…,A
）=（,,…,）B
（,,…,）=（
,,…,
）X
由上面三式即可得出结论.方法是:将第三式作线性变换A,结合一式,比较二式从而将它们联系起来……
注:定理4 告诉我们，同一个线性变换A在不同基下的矩阵之间的关系.
五．矩阵的相似
1．定义3
设A，B为数域P上两个n级方阵，如果可以找到数域P上的n级可逆方阵X，使得，称A相似于B，记作
.
2．相似关系的性质：
（1）反身性
（2） 对称性
（3）传递性
3．定理5 线性变换在不同基下所对应的矩阵是相似的；反过来，如果两个矩阵相似，那么它们可以看作同一个线性变换在两组基下所对应的矩阵.
4．几个结论
如果
,
，那么
(1)
,
(2)
由此可知，如果，且f
(x)是数域P上一多项式，那么
(3)
注:利用矩阵相似的这个性质可以简化矩阵的计算.
例2
设V是数域P上一个二维线性空间，
是一组基，线性变换A在下的矩阵是
计算A在V的另一组基
下的矩阵，这里
,A=,根据,可得B=
瀚海代数精品课程网资源 （需要原word文档请联系：nchy_zouzij@163.com）