§6子空间的交与和   <<返回

一．子空间的交

1.定理5 若,是线性空间V的两个子空间，则它们的交也是V的子空间.

证明：根据上一节定理2,证明两个封闭性……

2.子空间的交适合下列运算规律：

(1)(交换律)， (2)（结合律）.

3．推广：由结合律，可以定义多个子空间的交：,它也是子空间.

思考：子空间的并为何不行？

    设，，非子空间

二.子空间的和

1.定义8 设,是线性空间V的子空间，所谓与的和，是指由所有能表示成,而的向量组成的子集合，记作.

2.定理6 如果,是线性空间V的子空间，那么它们的和也是V的子空间.

证明：与定理5的证明方法一样……

3.子空间的和适合下列运算规律：

(1)(交换律)，  (2)（结合律）.

4．推广：多个子空间的和.它是由所有表示成

的向量组成的子空间.

三.关于子空间的交与和有以下结论：

1. 设都是子空间，那么由与可推出；而由与可推出.

2. 对于子空间与，以下三个论断是等价的：

1） 2) ;  3).  (给同学们自己练习)

例1 在三维几何中用表示一条通过原点的直线，表示一张通过原点而且与垂直的平面，那么，与的交是，而与的和是整个空间.

例2 在线性空间中，用与分别表示齐次方程组

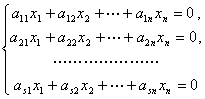   与 

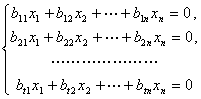
的解空间，那么就是齐次方程组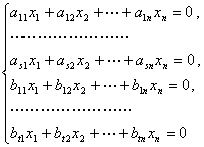的解空间.

例3 在线性空间V中，有

证明：只要证明集合相等即可。

3.两个子空间的交与和的维数.

定理7（维数公式）如果，是线性空间V的两个子空间，那么

维（）+维（）=维（）+维（）.

证明：先设，， 的维数。然后设出的一组基.将此基分别拓展成 与的基: 与

    下面只要证明T:是的一组基。

     1）易证T 能表示，2）证明T线性无关。这里有一点技巧：设有等式：

令.由上面等式易见

 设出在的表达式后可消去……

推论 如果n维线性空间V中两个子空间，的维数之和大于n，那么，必含有非零的公共向量.

     瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）