§4 基变换与坐标变换   <<返回

一、问题:设与是n维线性空间V中两组基，它们的关系是

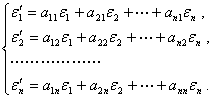                         (1)

设向量 在这两组基下的坐标分别是 与 ，即

             (2)

现在的问题就是找出与的关系.

首先指出，(1)中各式的系数实际上就是第二组基向量在第一组基下的坐标.向量的线性无关性就保证了(1)中系数矩阵的行列式不为零.换句话说，这个矩阵是可逆的.

二、基变换下的坐标表示

1．基变换的矩阵表示：把向量写成

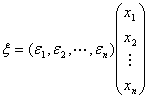,                              (3)

也就是把基写成一个 矩阵，把向量的坐标写成一个 矩阵，而把向量看作是这两个矩阵的乘积.

相仿地，(1)可以写成

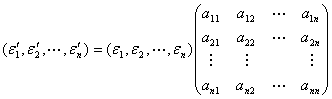.               (4)

2．矩阵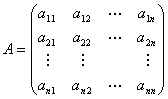称为由基到的过渡矩阵。

3．运算规律.

设和是V中两个向量组，是两个矩阵，那么       

4、基变换下坐标的变换式

现在回到本节所要解决的问题上来.由(2)有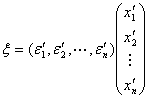.用(4)代入，得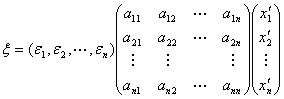.与(3)比较，由基向量的线性无关性，得

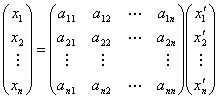,                     (5)

或者

.                    (6)

(5)与(6)给出了在基变换(4)下，向量的坐标变换公式.

例1  在§3例2 中有

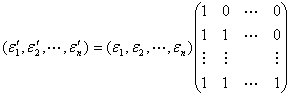
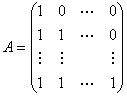就是过渡矩阵.不难得出

.

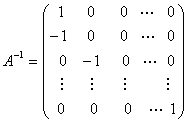因此                        

也就是.与§3所得出的结果是一致的.

例2  取的两个彼此正交的单位向量它们作成的一个基.令分别是由旋转角所得的向量，则也是的一个基，有

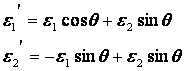
所以

｛ ｝到｛｝的过渡矩阵是.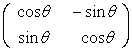

设 的一个向量 关于基｛｝和｛｝的坐标分别为 与().于是由(5)得           

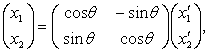
即            

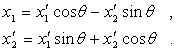
这正是平面解析几何里旋转坐标轴的坐标变换公式.

        瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）