§3  维数·基与坐标   <<返回

一、向量的线性相关与线性无关的概念

1.定义2  设V是数域P上的一个线性空间，是V一组向量,是数域P中的数，那么向量称为向量组的一个线性组合，有时也说向量可以用向量组线性表出.

2.定义3  设;                               (1)

                                  (2)

是V中两个向量组，如果（1）中每个向量都可以用向量组（2）线性表出，那么称向量（1）可以用向量组（2）线性表出.如果（1）与（2）可以互相线性表出，那么向量组（1）与（2）称为等价的.

3.定义4 线性空间V中向量称为线性相关，如果在数域P中有r个不全为零的数，使

.                       (3)

如果向量不线性相关，就称为线性无关.换句话说，向量组称为线性无关，如果等式（3）只有在时才成立.

二.几个常用的结论：

1. 单个向量线性相关的充要条件是.两个以上的向量线性相关的充要条件是其中有一个向量是其余向量的线性组合.

2. 如果向量组线性无关，而且可以被线性表出，那么.由此推出，两个等价的线性无关的向量组，必含有相同个数的向量.

3. 如果向量组线性无关，但线性相关，那么可以由被线性表出，而且表示法是唯一的.

在一个线性空间中究竟最多能有几个线性无关的向量，是线性空间的一个重要属性.

注：这里的概念和结论与上学期的相关结论是完全平行的。只是范围更广了。

三.维数、基与坐标n

１．定义5 如果在线性空间V中有n个线性无关的向量，但是没有更多数目的线性无关的向量，那么V就称为n维的；如果在V中可以找到任意多个线性无关的向量，那么V就称为无限维的.

２.定义6 在n维线性空间V中，n个线性无关的向量称为V的一组基.设是V中任一向量，于是线性相关，则可以被基线性表出：

.

其中系数是被向量和基唯一确定的，这组数就称为在基下的坐标，记为.

由以上定义看来，在给出空间V的一组基之前，必须先确定V的维数.

四．维数与基的判断

定理1 如果在线性空间V中有n个线性无关的向量，且V中任一向量都可以用它们线性表出，那么V是n维的，而就是V的一组基.

证明：只须证明n+1个向量必相关。

例1  在线性空间中，是n个线性无关的向量，而且每一个次数小于n的数域P上的多项式都可以被它们线性表出，所以是n维的，而就是它的一组基.

例2 在n维空间中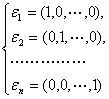，是一组基.对于任一向量,

有.所以 就是向量 在这组基

下的坐标.

例3 如果把复数域K看作是自身上的线性空间，那么它是一维的，数1就是一组基。作为是实数域上的线性空间，那么就是二维的，数1与i就是一组基.这个例子告诉我们，

注：维数是和所考虑的数域有关的.

    瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）