§4 正定二次型 <<返回
一、正定与半正定二次型
1.定义4
![]() 是实二次型,如果对于任意一组不全为零的实数
是实二次型,如果对于任意一组不全为零的实数![]()
(1)都有![]() .
.![]() 称为正定的
称为正定的
(2)
都有![]() ,那么
,那么![]() 称为负定的
称为负定的
(3)
都有![]() ,那么
,那么![]() 称为半正定的
称为半正定的
不定的…….
2.定义5
实对称矩阵A称为正定的,如果二次型![]() 正定.
正定.
3.几个基本的结论
(1)实二次型![]() 是正定的当且仅当
是正定的当且仅当![]() .
.
(2)非退化实线性替换保持正定性不变.
分析:设实二次型
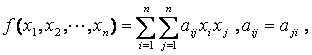 (1)
(1)
是正定的,经过非退化实线性替换![]() (2)
(2)
变成二次型
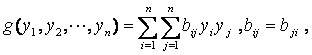 (3)
(3)
则![]() 的二次型
的二次型![]() 也是正定的,或者说,对于任意一组不全为零的实数
也是正定的,或者说,对于任意一组不全为零的实数![]() 都有
都有![]() .
.
因为二次型(3)也可以经非退化实线性替换![]() 变成二次型(1),所以按同样理由,当(3)正定时(1)也正定.
变成二次型(1),所以按同样理由,当(3)正定时(1)也正定.
二、正定与半正定二次型的判别
1. 法一
定理6
实数域上二次型![]() 是正定的
是正定的![]() 它的正惯性指数等于
它的正惯性指数等于![]() .
.
证明:只要将二次型化成标准型即可看出……
定理6说明,正定二次型![]() 的规范形为
的规范形为
![]() (5)
(5)
因为二次型(5)的矩阵是单位矩阵,所以实对称矩阵是正定的![]() 它与单位矩阵合同.
它与单位矩阵合同.
推论 正定矩阵的行列式大于零.
证明:根据正定矩阵与单位矩阵合同……
2.法2
(1)定义6
子式 称为矩阵
称为矩阵![]() 的顺序主子式.
的顺序主子式.
(2)定理7
实二次型![]() 是正定的
是正定的![]() 矩阵
矩阵![]() 的顺序主子式全大于零.
的顺序主子式全大于零.
证明:必要性:注意到k阶顺序主子式对应实二次型中![]() 均为零的情况……
均为零的情况……
充分性:对n用数学归纳法:第二步n元二次型时,证它与单位矩阵合同.
据归纳假设对n-1阶主子式![]() ,有可逆的n-1阶矩阵G,使
,有可逆的n-1阶矩阵G,使![]() .令
.令
![]()
再令![]() 其中
其中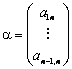 (关键!)此时有
(关键!)此时有
![]()
…![]() …
…
例
判定二次型![]() 是否正定.
(正定)
是否正定.
(正定)
3.负定二次型的判别:![]() 是正定的.
是正定的.
4.半正定的判别
定理8
对于二次型![]() ,其中
,其中![]() 是实对称的,下列条件等价:
是实对称的,下列条件等价:
(1)![]() 是半正定的;
是半正定的;
(2)它的正惯性指数与秩相等;
(3)有可逆实矩阵![]() ,使
,使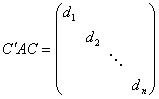 其中
其中![]() ;
;
(4)有实矩阵![]() 使
使
![]() .
.
(5)![]() 的所有主子式皆大于或等于零;
的所有主子式皆大于或等于零;
注:在(5)中,仅有顺序主子式大于或等于零是不能保证半正定性的.比如
![]()
就是一个反例.
证明
![]() 设
设![]() 的主子式全大于或等于零,
的主子式全大于或等于零,![]() 是
是![]() 的
的![]() 级顺序主子式,
级顺序主子式,![]() 是对应的矩阵
是对应的矩阵
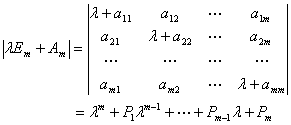
其中![]() 是
是![]() 中一切
中一切![]() 级主子式之和,由题设
级主子式之和,由题设![]() ,故当
,故当![]() 时,
时,![]() ,
,![]() 是正定矩阵.
是正定矩阵.
若![]() 不是半正定矩阵,则存在一个非零向量
不是半正定矩阵,则存在一个非零向量![]() ,使
,使
![]()
令
![]()
![]()
与![]() 时
时![]() 是正定矩阵矛盾,故
是正定矩阵矛盾,故![]() 是半正定矩阵.
是半正定矩阵.
Th8![]() 记
记![]() 的行指标和列指标为
的行指标和列指标为![]() 的
的![]() 级主子式为
级主子式为![]() ,对应矩阵是
,对应矩阵是![]() ,对任意
,对任意![]() ,有
,有![]() ,其中
,其中
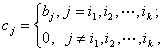
又![]() 是半正定矩阵,从而
是半正定矩阵,从而
![]() .
.
若![]() ,则P234,12T,存在
,则P234,12T,存在![]() 使
使![]() 与
与![]() 矛盾,所以
矛盾,所以![]() .
.
◇设![]() 为
为![]() 级实矩阵,且
级实矩阵,且![]() ,则
,则![]() 都是正定矩阵.
都是正定矩阵.
◇设![]() 为
为![]() 实矩阵,则
实矩阵,则![]() 都是半正定矩阵.
都是半正定矩阵.
证明
![]() 是实对称矩阵,
是实对称矩阵,![]() 令
令![]() ,则
,则![]() 是
是![]() 维实向量
维实向量![]()
![]()
![]() 是半正定矩阵,同理可证
是半正定矩阵,同理可证![]() 是半正定矩阵.
是半正定矩阵.
◇设![]() 是
是![]() 级正定矩阵,则
级正定矩阵,则![]() 时,
时,![]() 都是正定矩阵.
都是正定矩阵.
证明
由于![]() 正定,存在可逆矩阵
正定,存在可逆矩阵![]() ,使
,使![]() ,
,![]() ,从而
,从而![]() 为正定矩阵.
为正定矩阵.![]()
![]() 正定
正定
又![]() 正定,
正定,![]() ,
,![]() 正定,
正定,![]() 正定.
正定.![]() 对称
对称
当![]() 时,
时,![]() ,从而
,从而![]() 正定.
正定.
当![]() 时,
时,
![]()
所以![]() 与
与![]() 合同,因而
合同,因而![]() 正定.
正定.
瀚海代数精品课程网资源 (需要原word文档请联系:nchy_zouzij@163.com)