§3 唯一性    <<返回

在一个二次型的标准形中，系数不为零的平方项的个数是唯一确定的，与所作的非退化线性替换无关，二次型矩阵的秩有时就称为二次型的秩.

至于标准形中的系数，就不是唯一确定的.在一般数域内，二次型的标准形不是唯一的，而与所作的非退化线性替换有关.

下面只就复数域与实数域的情形来进一步讨论唯一性的问题.

一、复数域上的二次型的唯一性

设是一个复系数的二次型，由本章定理1，经过一适当的非退化线性替换后，变成标准形，不妨假定化的标准形是

.            (1)

易知就是的矩阵的秩.因为复数总可以开平方，再作一非退化线性替换

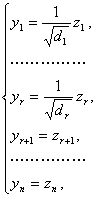                                             (2)

(1)就变成                                          (3)

(3)称为复二次型 的规范形.规范形完全被原二次型矩阵的秩所决定，因此有

定理3 任意一个复系数的二次型经过一适当的非退化线性替换可以变成唯一的规范形..从而有两个复数对称矩阵合同的充要条件是它们的秩相等.

    二、实数域上二次型的唯一性

设是一实系数的二次型.由本章定理1，经过某一个非退化线性替换，再适当排列文字的次序，可使变成标准形

                            (4)

其中 是 的矩阵的秩.因为在实数域中，正实数总可以开平方，所以再作一非退化线性替换

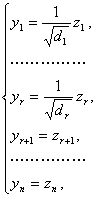                            (5)

(4) 就变成                       (6)

(6)就称为实二次型 的规范形.显然规范形完全被 这两个数所决定.

    三.惯性定理

1.定理4(惯性定理).任意一个实数域上的二次型，经过一适当的非退化线性替换可以变成规范形，且规范形是唯一的.

证明:前部分上面已证,只须证唯一性.

反证,设f有两种替换分别化为(*)与(**).两式相等.设.

一方面,由可知两组向量间的关系.令.

另一方面,从正定二次型得启发,先让为零,现在的问题是能否找到的一组非零值使(*)式>0,而对应(**)式.进一步,让=0?这从中对应的前q行 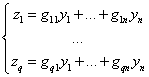 可得到解答……

2.定义3 在实二次型 的规范形中，正平方项的个数 称为 的正惯性指数；负平方项的个数 称为 的负惯性指数；它们的差 称为 的符号差.

3.定理5 （1）任一复对称矩阵都合同于一个下述形式的对角矩阵：.

其中对角线上1 的个数等于的秩.

（2）任一实对称矩阵都合同于一个下述形式的对角矩阵：,

其中对角线上1的个数 及-1的个数 （ 等于 的秩）都是唯一确定的，分别称为 的正、负惯性指数，它们的差 称为 的符号差..

        瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）