§2 标准形 <<返回
一、二次型的标准型
1.
二次型![]() 经过非退化线性替换所变成的平方和形式
.
经过非退化线性替换所变成的平方和形式
. ![]() (1)
(1)
称为![]() 的标准形.
的标准形.
2.
定理1
数域![]() 上任意一个二次型都可以经过非化线性替换变成平方和(1)的形式.
上任意一个二次型都可以经过非化线性替换变成平方和(1)的形式.
证明:用中学所学的“配方法”证明.对n用数学归纳法.
第二步,分三种情形讨论:1)![]() 中至少一个不为零,设
中至少一个不为零,设![]() .先将含
.先将含![]() 的项配方后成平方的形式,余项不含
的项配方后成平方的形式,余项不含![]() .再用线性替换将平方项替换…2)所有
.再用线性替换将平方项替换…2)所有![]() 为零,但至少有一个
为零,但至少有一个![]() ,设
,设![]() .此时先设
.此时先设![]() ,变出平方和后同1)…3)含
,变出平方和后同1)…3)含![]() 的系数全为零.据归纳假设直接得…
的系数全为零.据归纳假设直接得…
易知,二次型(1)的矩阵是对角矩阵,

反过来,矩阵为对角形的二次型就只包含平方项.按上一节的讨论,经过非退化的线性替换,二次型的矩阵变到一个合同的矩阵,因此定理1可以叙述为:
定理2
在数域![]() 上,任意一个对称矩阵都合同于一对角矩阵.
上,任意一个对称矩阵都合同于一对角矩阵.
例1
化二次型![]() 为标准形.
为标准形.
(结论: .)
.)
例2 完全用矩阵的方法做上题…….
二、配方法
1.![]() 这时的变量替换为
这时的变量替换为
令
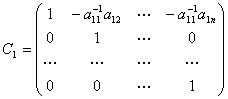 ,
,
则上述变量替换相应于合同变换![]() .为计算
.为计算![]() ,可令
,可令
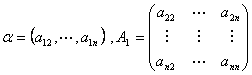 .
.
于是![]() 和
和![]() 可写成分块矩阵
可写成分块矩阵
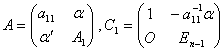 ,这样
,这样
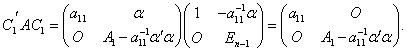
矩阵![]() 是一个
是一个![]() 对称矩阵,由归纳法假定,有
对称矩阵,由归纳法假定,有![]() 可逆矩阵
可逆矩阵![]() 使
使![]() 为对角形,令
为对角形,令![]() ,于是
,于是
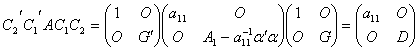 ,
,
这是一个对角矩阵,我们所要的可逆矩阵就是![]() .
.
2.
![]() 但只有一个
但只有一个![]() .
.
这时,只要把![]() 的第一行与第
的第一行与第![]() 行互换,再把第一列与第
行互换,再把第一列与第![]() 列互换,就归结成上面的情形,根据初等矩阵与初等变换的关系,取
列互换,就归结成上面的情形,根据初等矩阵与初等变换的关系,取
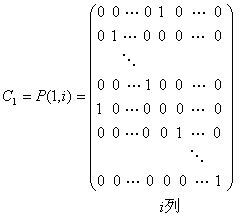
![]() 行
行
显然
![]() .矩阵
.矩阵![]() 就是把
就是把![]() 的第一行与第
的第一行与第![]() 行互换,再把第一列与第
行互换,再把第一列与第![]() 列互换.因此,
列互换.因此,![]() 左上角第一个元素就是
左上角第一个元素就是![]() ,这样
,这样
就归结到第一种情形.
3.
![]() 但有一
但有一![]()
与上一情形类似,作合同变换
![]() 可以把
可以把![]() 搬到第一行第二列的位置,这样就变成了配方法中的第二种情形.与那里的变量替换相对应,取
搬到第一行第二列的位置,这样就变成了配方法中的第二种情形.与那里的变量替换相对应,取
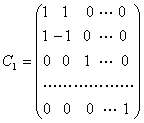 ,
,
于是![]() 的左上角就是
的左上角就是
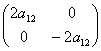 ,也就归结到第一种情形.
,也就归结到第一种情形.
4.
![]()
由对称性,![]() 也全为零.于是
也全为零.于是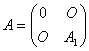 ,
,
![]() 是
是![]() 级对称矩阵.由归纳法假定,有
级对称矩阵.由归纳法假定,有![]() 可逆矩阵
可逆矩阵![]() 使
使![]() 成对角形.取
成对角形.取![]() ,
,![]() 就成对角形.
就成对角形.
例
化二次型![]() 成标准形.
成标准形.
(替换:X=CY.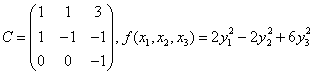 .)
.)
瀚海代数精品课程网资源 (需要原word文档请联系:nchy_zouzij@163.com)