§1 二次型及其矩阵表示  <<返回

一、二次型及其矩阵表示

1.设是一个数域,一个系数在中的的二次齐次多项式

称为数域 上的一个元二次型，简称二次型.

2.定义1 设是两组文字，系数在数域P中的一组关系式

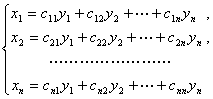                      (2)

称为由 到 的一个线性替换，或简称线性替换.如果系数行列式,那么线性替换(2)就称为非退化的.

3.二次型的矩阵表示

令由于所以二次型(1)可写成

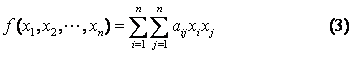
把(3)的系数排成一个矩阵                    (4)

它称为二次型(3)的矩阵.因为 所以.把这样的矩阵称为对称矩阵，因此，二次型的矩阵都是对称的.令

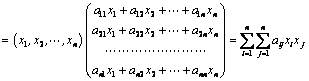
或

应该看到二次型(1)的矩阵A的元素,当时正是它的项的系数的一半,而是项的系数，因此二次型和它的矩阵是相互唯一决定的.由此可得,若二次型

且,则.

4.结论:线性替换把二次型变成二次型.

二、矩阵的合同关系

1.分析

令 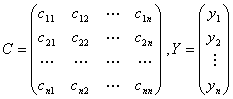,于是线性替换（4）可以写成

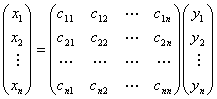
或者                             .

设                             (7)

是一个二次型，作非退化线性替换                             (8)

得到一个的二次型     ，

把（8）代入（7），有

易看出，矩阵 也是对称的，由此即得.这是前后两个二次型的矩阵的关系。

2.定义2 数域P上两个阶矩阵，称为合同的，如果有数域P上可逆的矩阵,使得.

3.合同关系的性质:1) 自反性…  2) 对称性…3) 传递性…

4.结论:经过非退化的线性替换，新二次型的矩阵与原来二次型的矩阵是合同的。

在变换二次型时，总是要求所作的线性替换是非退化的。一般地，当线性替换

是非退化时，由上面的关系即得

.

这也是一个线性替换，它把所得的二次型还原.这样就使我们从所得二次型的性质可以推知原来二次型的一些性质.

        瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）