§7 分块乘法的初等变换及应用举例 <<返回
将分块乘法与初等变换结合是矩阵运算中的重要手段.
现设某个单位矩阵如下进行分块:
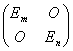 .
.
对它进行两行(列)对换;某一行(列)左乘(右乘)一个矩阵![]() ;一行(列)加上另一行(列)的
;一行(列)加上另一行(列)的![]() (矩阵)倍数,就可得到如下类型的一些矩阵:
(矩阵)倍数,就可得到如下类型的一些矩阵:
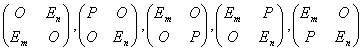 .
.
和初等矩阵与初等变换的关系一样,用这些矩阵左乘任一个分块矩阵
![]() ,
,
只要分块乘法能够进行,其结果就是对它进行相应的变换:
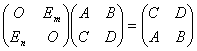 ,
(1)
,
(1)
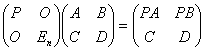 ,
(2)
,
(2)
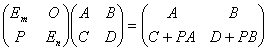 .
(3)
.
(3)
同样,用它们右乘任一矩阵,进行分块乘法时也有相应的结果.
在(3)中,适当选择![]() ,可使
,可使![]() .例如
.例如![]() 可逆时,选
可逆时,选![]() ,则
,则![]() .于是(3)的右端成为
.于是(3)的右端成为
![]()
这种形状的矩阵在求行列式、逆矩阵和解决其它问题时是比较方便的,因此(3)中的运算非常有用.
例1
设![]() ,
,![]() 可逆,求
可逆,求![]() .(结论:
.(结论:![]() )
)
例2
证明行列式的乘积公式![]() .
.
证明:据第二章第6节例3.已有如下
![]()
现在的问题就是证明![]() .先对左式对应的矩阵作左乘
.先对左式对应的矩阵作左乘
![]()
可发现![]() 相当于对做若干次初等行变换……因此得
相当于对做若干次初等行变换……因此得
![]() .
.
所以问题变为证![]() .只要对左式左边再做若干次行对换成为
.只要对左式左边再做若干次行对换成为![]() 即可……
即可……
例3
设![]() ,且
,且

则有下三角形矩阵![]() 使
使![]() =上三角形矩阵.
=上三角形矩阵.
证明:对n用数学归纳法:将n级矩阵A分成四块:
![]()
先据归纳假设将![]() 化成上三角型:
化成上三角型:![]() 上三角型.然后将A左乘
上三角型.然后将A左乘![]() 目的是将左下角变成0.再左乘
目的是将左下角变成0.再左乘![]() ,目的是将
,目的是将![]() 化成上三角型.两矩阵相乘即可得
化成上三角型.两矩阵相乘即可得![]() …
…
瀚海代数精品课程网资源 (需要原word文档请联系:nchy_zouzij@163.com)