§5 矩阵的分块 <<返回
一.引例.在矩阵
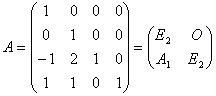 …
…
.
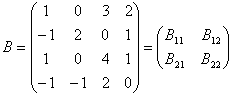 …
…
在计算![]() 时,把
时,把![]() 都看成是由这些小矩阵组成的,即按2级矩阵来运算.于是
都看成是由这些小矩阵组成的,即按2级矩阵来运算.于是
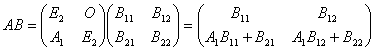 ,
,
其中
![]() ,
,
![]() .
.
因之
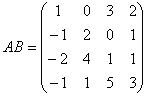 .不难验证,直接按4级矩阵乘积的定义来作,结果是一样的.
.不难验证,直接按4级矩阵乘积的定义来作,结果是一样的.
二.分块矩阵的乘法
一般,设![]() ,把
,把![]() 分成一些小矩阵
分成一些小矩阵
 ,
(1)
,
(1)
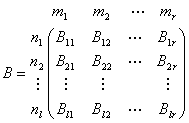 ,
(2)
,
(2)
其中每个![]() 是
是![]() 小矩阵,每个
小矩阵,每个![]() 是
是![]() 小矩阵,于是有
小矩阵,于是有
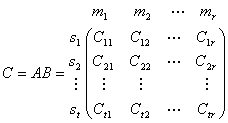 ,
(3)
,
(3)
其中
![]() . (4)
. (4)
这个结果是由矩阵乘积的定义直接验证即得.
应该注意,在分块(1),(2)中矩阵的列的分法必须与矩阵的行的分法一致.
以下会看到,分块乘法有许多方便之处.常常在分块之后,矩阵间相互的关系看得更清.
实际上,在证明关于矩阵乘积的秩的定理时,已经用了矩阵分块的想法.在那里,用![]() 表示
表示![]() 的行向量,于是
的行向量,于是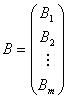 ,这就是
,这就是![]() 的一种分块.按分块相乘,就有
的一种分块.按分块相乘,就有
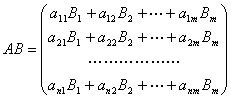 .
.
用这个式子很容易看出![]() 的行向量是
的行向量是![]() 的行向量的线性组合;将
的行向量的线性组合;将![]() 进行另一种分块乘法,从结果中可以看出
进行另一种分块乘法,从结果中可以看出![]() 的列向量是
的列向量是![]() 的列向量的线性组合.
的列向量的线性组合.
例:求矩阵
的逆矩阵,其中![]() 分别是
分别是![]() 级和
级和![]() 级的可逆矩阵,
级的可逆矩阵,![]() 是
是![]() 矩阵,
矩阵,![]() 是
是![]() 零矩阵.
零矩阵.
首先,因为![]() ,所以当
,所以当![]() 可逆时,
可逆时,![]() 也可逆.设
也可逆.设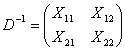 ,
,
于是
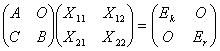 ,
,
这里![]() 分别表示
分别表示![]() 级和
级和![]() 级单位矩阵.乘出来并比较等式两边,得
级单位矩阵.乘出来并比较等式两边,得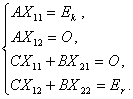
……
.因此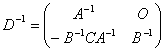 .特别地,当
.特别地,当![]() 时,有
时,有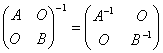 .
.
三.常见的分块
1.有关方程组的 (1)增广矩阵… (2)行向量分块… (3)列向量分块…
2.有关对角阵的乘法 (1)左乘… (2)右乘…
四.准对角阵的运算
1.概念
形式为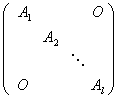 的矩阵,其中
的矩阵,其中![]() 是
是![]() 矩阵
矩阵![]() ,通常称为准对角矩阵.
,通常称为准对角矩阵.
2.运算(1)积:对于两个有相同分块的准对角矩阵
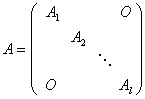 ,
,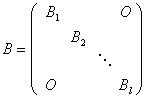 ,
,
如果它们相应的分块是同级的,那么显然有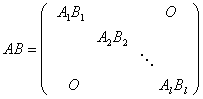
(2)和: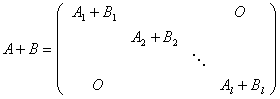 它们还是准对角矩阵.
它们还是准对角矩阵.
(3)逆:其次,如果![]() 都是可逆矩阵,那么
都是可逆矩阵,那么
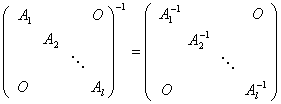 .
.
瀚海代数精品课程网资源 (需要原word文档请联系:nchy_zouzij@163.com)