§4  矩阵的逆    <<返回

一、可逆矩阵的概念

在§2我们看到，矩阵与复数相仿，有加、减、乘三种运算.矩阵的乘法是否也和复数一样有逆运算呢？这就是本节所要讨论的问题.

对于任意的级方阵都有这里是级单位矩阵.因之，从乘法的角度来看，级单位矩阵在级方阵中的地位类似于1在复数中的地位.一个复数的倒数可以用等式来刻划，相仿地，我们引入

1.定义7 级方阵称为可逆的，如果有级方阵，使得

,                       (1)

这里是级单位矩阵.

注:由于矩阵的乘法规则，只有方阵才能满足(1).其次，对于任意的矩阵，适合等式(1)的矩阵是唯一的(如果有的话).

2.定义8 如果矩阵适合(1)，那么就称为的逆矩阵，记为.

二、可逆矩阵的逆矩阵的求法

下面要解决的问题是：在什么条件下矩阵是可逆的？如果可逆，怎样求？

1.定义9 设是矩阵            

中元素的代数余子式，矩阵称为矩阵的伴随矩阵.

由行列式按一行(列)展开的公式立即得出：

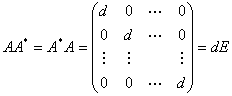,               (2)

其中.

如果，那么由(2)得

.                        (3)

2.定理3 矩阵可逆的充要条件是非退化的，而

    证明:由可逆的定义与上面的分析……

根据定理3容易看出，对于级方阵，如果那么就都是可逆的并且它们互为逆矩阵.

定理3不但给出了一矩阵可逆的条件，同时也给出了求逆矩阵的公式.按这个公式来求逆矩阵，计算量一般是非常大的.在以后我们将给出另一种求法.

可以看出，如果，那么

推论 如果矩阵可逆，那么与也可逆，且

            .

    证明:根据概念直接求得……

    例1:求矩阵的逆阵.   (结论:为)

    例2:求矩阵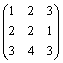的逆阵.   (结论:为)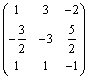

三.克拉默法则的另一种推导法.

线性方程组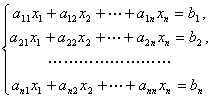

可以写成                              .                     (6)

如果，那么可逆.用代入(6)，得恒等式，这就是说是一个解.

如果是(6)的一个解，那么由得,

即 .这就是说，解是唯一的.用的公式代入，乘出来即克拉默法则中给出的公式.

定理4 是一个矩阵，如果是可逆矩阵，是可逆矩阵，那么

秩（）=秩（）=秩（）.

    证明:根据上一节定理2以及令.且……

       瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）