§2 矩阵的运算 <<返回
现在来定义矩阵的运算.以下所讨论的矩阵全是由某数域中的数组成的.
一. 加法
1.定义1
设![]() ,
,![]() 是两个
是两个![]() 矩阵,则矩阵
矩阵,则矩阵![]() 称为
称为![]() 和
和![]() 的和,记为
的和,记为![]() .
.
注:相加的矩阵必须要有相同的行数和列数(同型).
2.性质
(1)结合律……; (2)交换律……
3.元素全为零的矩阵称为零矩阵,记为![]() ,在不致引起含混的时候,可简单地记为
,在不致引起含混的时候,可简单地记为![]() .显然,对所有的
.显然,对所有的![]() ,
,![]() .
.
负矩阵…...矩阵的减法…
例: 在§1,3中可引出两种物资的总调动方案的求法即求矩阵的和……
4.矩阵相加的秩:根据矩阵加法的定义应用关于向量组的秩的性质,容易看出:
秩(![]() +
+![]() )≤
秩(
)≤
秩(![]() )+秩(
)+秩(![]() )
)
二. 乘法
1.引例:设![]() 和
和![]() 是两组变量,它们之间的关系为
是两组变量,它们之间的关系为
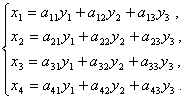 (1)
(1)
又如![]() 是第三组变量,它们与
是第三组变量,它们与![]() 的关系为
的关系为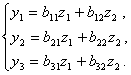 (2)
(2)
由(1)与(2)不难看出![]() 与
与![]() 的关系:
的关系:
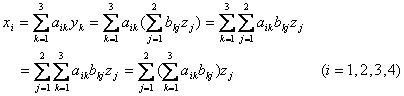 .
(3)
.
(3)
如果我们用![]() (4)
(4)
来表示![]() 与
与![]() 的关系,比较(3),(4),就有
的关系,比较(3),(4),就有
![]() .
(5)
.
(5)
用矩阵的表示法,我们可以说,如果矩阵![]() 分别表示变量
分别表示变量![]() 与
与![]() 以及
以及![]() 与
与![]() 之间的关系,那么表示
之间的关系,那么表示![]() 与
与![]() 之间的关系的矩阵
之间的关系的矩阵![]() 就由公式(5)决定.矩阵
就由公式(5)决定.矩阵![]() 称为矩阵
称为矩阵![]() 与
与![]() 的乘积,记为
的乘积,记为![]()
2.定义2
设![]() ,那么矩阵
,那么矩阵![]() ,其中
,其中
![]() ,
(6)
,
(6)
称为矩阵![]() 与
与![]() 的乘积,记为
的乘积,记为![]() .
.
注:在乘积的定义中,我们要求第二个矩阵的行数与第一个矩阵的列数相等.
例1
设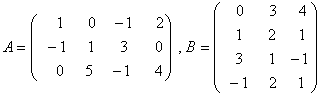 ,那么
,那么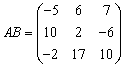
例2
如果![]() 是一线性方程组的系数矩阵,而
是一线性方程组的系数矩阵,而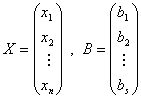
分别是未知量和常数项所成的矩阵,那么线性方程组就可以写成矩阵的等式![]() .
.
例3
设由坐标系![]() 到
到![]() 的坐标变换的矩阵为
的坐标变换的矩阵为
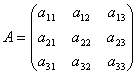 .若令
.若令
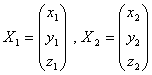 ,那么坐标变换的公式为
,那么坐标变换的公式为![]() .
.
如果再作一次坐标系的转轴,设由第二个坐标系
![]() 到第三个坐标系
到第三个坐标系
![]() 的坐标变换公式为
的坐标变换公式为
![]() ,其中
,其中
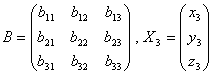 .那么不难看出,由第一个坐标系到第三个坐标系的坐标变换的矩阵即为
.那么不难看出,由第一个坐标系到第三个坐标系的坐标变换的矩阵即为
![]() .
.
3.运算律
(1)结合律……. (2)分配律(分左右),
注:矩阵的乘法不适合交换律,即一般说来![]() .
.
例:设![]()
![]() ,
而
,
而![]() .
.
由这个例子我们还可看出,两个不为零的矩阵的乘积可以是零,这是矩阵乘法的一个特点.由此还可得出矩阵消去律不成立.即当![]() 时,不一定有
时,不一定有![]() .
.
定义3
![]() 矩阵
矩阵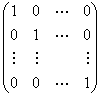 称为
称为![]() 级单位矩阵,记为
级单位矩阵,记为![]() ,或者在不致引起含混的时候简单写为
,或者在不致引起含混的时候简单写为![]() .显然有
.显然有![]() ,
,
![]() .
.
应该指出,由于矩阵无交换律,所以(9)与(10)是两条不同的规律.
我们还可以定义矩阵的方幂.设![]() 是一
是一![]() 矩阵,定义
矩阵,定义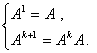 当然只能对行数与列数相等的矩阵来定义.由乘法的结合律,不难证明
当然只能对行数与列数相等的矩阵来定义.由乘法的结合律,不难证明![]() ,
,
![]() .
.
这里![]() 是任意正整数.因为矩阵乘法不适合交换律,所以
是任意正整数.因为矩阵乘法不适合交换律,所以![]() 与
与![]() 一般不相等.
一般不相等.
三. 数量乘法
. 1.定义4
矩阵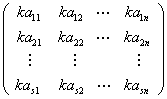 称矩阵
称矩阵![]() 与数
与数![]() 的数量乘积,记
的数量乘积,记![]() .
.
2.运算律:(1).![]() ,
(2)
,
(2)![]() ,
,
(3)![]() ,
(4)
,
(4)![]() ,
(5)
,
(5)![]() .
.
3.数量矩阵:矩阵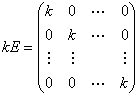 通常称为数量矩阵.作为(5)的特殊情形,如果
通常称为数量矩阵.作为(5)的特殊情形,如果![]() 是一
是一![]() 矩阵,那么有
矩阵,那么有![]()
此式说明,数量矩阵与所有的![]() 矩阵作乘法是可交换的.可以证明:如果一个
矩阵作乘法是可交换的.可以证明:如果一个![]() 级矩阵与所有
级矩阵与所有![]() 级矩阵作乘法是可交换的,则这个矩阵必为数量矩阵.又有
级矩阵作乘法是可交换的,则这个矩阵必为数量矩阵.又有![]() ,
,
![]() (数量矩阵的加法与乘法完全归结为数的加法与乘法).
(数量矩阵的加法与乘法完全归结为数的加法与乘法).
四. 转置
1.定义5
设![]() ,A的转置为
,A的转置为![]() .
.
2.运算律:
(1)![]() ,
(2).
,
(2).![]() ,
(3).
,
(3).![]() ,
(4).
,
(4).![]() .
.
例4
设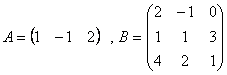 .求
.求![]() .
.
(结论:![]() )
)
瀚海代数精品课程网资源 (需要原word文档请联系:nchy_zouzij@163.com)