§5 线性方程组有解判别定理   <<返回

一、向量方程

设线性方程组为                    (1)

引入向量        .         (2)

于是线性方程组(1)可以改写成向量方程

.                         (3)

线性方程组(1)有解的充要条件为向量可以表成向量组的线性组合.

二、线性方程组(1)有解的进一步判别

定理7　 线性方程组(1)有解的充要条件为它的系数矩阵A与增广矩阵                 有相同的秩.

证明:充分性:有解说明可由线性表示.从而与 有相同的秩……必要性: A与的列向量有相同的最大无关组,从而与等价……

这个判别条件与以前的消元法一致.用消元法解线性方程组(1)的第一步就是用初等行变换把增广矩阵化成阶梯形.这个阶梯形矩阵在适当调动前列的顺序之后可能有两种情形：

或者

其中.在前一种情形，原方程组无解，而在后一种情形方程组有解.实际上，把这个阶梯形矩阵最后一列去掉，那就是线性方程组(1)的系数矩阵经过初等行变换所化成的阶梯形.这就是说，当系数矩阵与增广矩阵的秩相等时，方程组有解；当增广矩阵的秩等于系数矩阵的秩加1时，方程组无解.

以上的说明可以认为是判别定理的另一个证明.

三、一般线性方程组的一个解法.

设线性方程组(1)有解，矩阵与的秩都等于，而是矩阵的一个不为零的级子式(当然它也是的一个不为零的子式)，为了方便起见，不妨设位于的左上角.

在这种情况下，的前行就是一个极大线性无关组，第行都可以经它们线性表出.因此，线性方程组(1)与

                (4)

同解.

当时，由克拉默法则，线性方程组(4)有唯一解，也就是线性方程组(1)有唯一解.

当时，将线性方程组(4)改写为

        (5)

(5)作为的一个方程组，它的系数行列式.由克拉默法则，对于的任意一组值，线性方程组(5)，也就是线性方程组(1)，都有唯一的解. 就是线性方程组(1)的一组自由未知量.对(5)用克拉默法则，可以解出：

                     (6)

(6)就是线性
方程组(1)的一般解 .

例 取怎样的数值时，线性方程组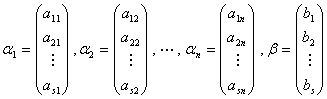有唯一解，没有解，有无穷多解？ (结论: =1:无穷多解. =-2:无解.其余有唯一解)

 瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）