§4 矩阵的秩  <<返回

一、矩阵的秩

1.矩阵与向量组的关系

如果把矩阵的每一行看成一个向量，那么矩阵就可以认为是由这些向量组成的.同样，如果把每一列看成一个向量，那么矩阵也可以认为是由列向量组成的.

2矩阵的行秩与列秩

1.定义15 所谓矩阵的行秩就是指矩阵的行向量组的秩；矩阵的列秩就是矩阵的列向量组的秩.

例:矩阵的行向量组是

它的秩是3.它的列向量组是

它的秩也是3.

2.问题:是否任意矩阵的行秩都等于列秩?

3.矩阵的秩

1.引理 如果齐次线性方程组

                      （1）

的系数矩阵A的行秩，那么它有非零解.

    证明:据矩阵与向量组的对应关系.找出与(1)同解的r个线性方程.再运用第一节定理1……

2.定理4 矩阵的行秩与列秩相等.

证明:先设.并设A的行秩r,列秩为r₁.先证.

据行秩为r,则其行向量有r个向量的最大无关组.它对应一个只有零解的齐次方程.由引理其系数矩阵的行秩.实际上,系数矩阵的行向量组的最大无关组即为A的某些列向量组的“缩短”……

同理可证.

3.因为行秩等于列秩，统称为矩阵的秩.

二、矩阵的秩与行列式的联系

定理5 矩阵              

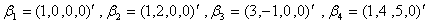
的行列式为零的充要条件是的秩小于.

     证明:充分性:由已知,A的行向量组线性相关.因此有一个向量能被其余向量线性表示.再结合行列式的性质,可将对应行变成零……

     必要性:对n用数学归纳法:…对n级为零的行列式.先设法利用行列式按列展开和行列式的性质,将A化成数乘n-1级行列式的形式.据归纳假设, n-1级行列式的行向量组线性相关,再由线性关系,推出原行向量组线性相关……

推论 齐次线性方程组有非零解的充要条件是它的系数矩阵A的行列式等于零.

    三、矩阵的子式与最高阶非零子式

1.定义16 在一个矩阵中任意选定行和列，位于这些选定的行和列的交点上的个元素按原来的次序所组成的级行列式，称为的一个级子式.

在定义中，当然有.

2.定理6 一矩阵的秩是的充要条件为矩阵中有一个级子式不为零，同时所有级子式全为零.

证明:必要性:利用矩阵行秩=列秩.根据定理5,可证任意级子式全为零.并可找出非零的级子式(先通过找行向量组的最大无关组去除一些行,再通过行秩=列秩去除相同数量的列…)

充分性:由必要性可推理……

从定理的证明可以看出，这个定理实际上包含两部分，一部分是，矩阵的秩的充要条件为有一个级子式不为零；另一部分是，矩阵的秩的充要条件为的所有级子式全为零.从定理的证明还可以看出，在秩为的矩阵中，不为零的级子式所在的行正是它行向量组的一个极大线性无关组，所在的列正是它列向量的一个极大线性无关组.

3.矩阵的最高阶非零子式…

四、矩阵的秩的计算

1.用求最高阶非零子式的方法算(较少用)…

2.矩阵化成阶梯形法.

(1)原理

首先，矩阵的初等行变换是把行向量组变成一个与之等价的向量组.等价的向量组有相同的秩，因此，初等行变换不改变矩阵的秩.同样初等列变换也不改变矩阵的秩.

其次，阶梯形矩阵的秩就等于其中非零的行的数目.

(2).方法:为了计算一个矩阵的秩，只要用初等行变换把它变成阶梯形，这个阶梯形矩阵中非零的行的个数就是原来矩阵的秩.

以上的讨论还说明，用初等变换化一个线性方程组成阶梯形，最后留下来的方程的个数与变换的过程无关，因为它就等于增广矩阵的秩.

例 利用初等变换求下面矩阵的秩：

.

(结论:2)

        瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）