§3  线性相关性   <<返回

一、线性表出与等价

1.定义9  向量称为向量组的一个线性组合，如果有数域中的数，使.. 也说可以经向量组线性表出. (叫做这个线性组合的系数)

例:任一个维向量都是向量组

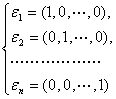                          （1）

的一个线性组合.向量 称为 维单位向量.

注：（１）零向量是任意向量组的线性组合.

（２）由定义，每一个向量组都可以经它自身线性表出

2.定义10  如果向量组中每一个向量都可以经向量组线性表出，那么向量组就称为可以经向量组线性表出.如果两个向量组互相可以线性表出，它们就称为等价.

3.向量组之间等价的性质:1）反身性…      2）对称性…    3）传递性…

二、线性相关与线性无关

1.概念

1)定义11  如果向量组中有一个向量是可以由其余的向量的线性表出，那么向量组线性相关. 否则称线性无关

从定义可以看出，任意一个包含零向量的向量组一定是线性相关的.向量组线性相关就表示或者(这两个式子不一定能同时成立).在为实数域，并且是三维时，就表示向量与共线.线性相关的几何意义就是它们共面….

2)定义11′向量组称为线性相关的，如果有数域中不全为零的数，使.

注:这两个定义在的时候是一致的. 定义11′包含了由一个向量组构成的向量组的情形. 单独一个零向量线性相关，单独一个非零向量线性无关.

3)线性无关的描述:向量组线性无关，即可以推出.

由定义，如果一向量组的一部分线性相关，那么这个向量组就线性相关.换句话说，如果一向量组线性无关，那么它的任何一个非空的部分组也线性无关.

2.线性相关性的基本判别法

要判断一个向量组                      (2)

是否线性相关，根据定义11，就是看方程             (3)

有无非零解.

结论:向量组线性无关的充要条件是齐次线性方程组(3)只有零解.

例1  判断的向量是否线性相关。(是)

例2  在向量空间里，对于任意非负整数,线性无关.

例3 若向量组线性无关，则向量组线性无关.            

如果向量组(2)线性无关，那么在每一个向量上添一个分量所得到的维的向量组                             (4)

也线性无关.

3.定理2 设与是两个向量组.如果

1）向量组可以经线性表出，     2） ，

那么向量组必线性相关.

    证明:根据定义证.用的表达式表达.最后化成判断齐次现性方程组是否有非零解的问题…….

推论1 如果向量组可以经向量组线性表出，且线性无关，那么.(这只是定理2换个说法…)

推论2 任意个维向量必线性相关.(因为它们都可以用线性表示)

推论3 两个线性无关的等价向量组必含有相同个数的向量.(正反两次用定理2即得)

定理2的几何意义：在三维向量的情形，如果，那么可以由向量线性表出的向量当然都在所在的平面上，因而这些向量是共面的，也就是说，当时，这些向量线性相关.两个向量组与等价，就意味着它们在同一平面上.

三、极大线性无关组与秩

1.定义13 一向量组的一个部分组称为一个极大线性无关组，如果这个部分组本身是线性无关的，并且从这个向量组中任意添一个向量(如果还有的话)，所得的部分向量组都线性相关.

一个线性无关向量组的极大线性无关组就是这个向量组本身.

2.极大线性无关组的一个基本性质:任意一个极大线性无关组都与向量组本身等价.

例4  看的向量组在这里｛｝线性无关，而，所以｛｝是一个极大线性无关组.另一方面，｛｝，｛｝也都是向量组｛｝的极大线性无关组.

由上面的例子可以看出，向量组的极大线性无关组不是唯一的.但是每一个极大线性无关组都与向量组本身等价，因而，一向量组的任意两个极大线性无关组都是等价的.

3. 向量组的秩

(1).定理3 向量组的极大线性无关组都含有相同个数的向量.(由定理2的推论3得)

定理3表明，极大线性无关组所含向量的个数与极大线性无关组的选择无关,因此有

(2).定义14 向量组的极大线性无关组所含向量的个数称为这个向量组的秩.

一向量组线性无关的充要条件是它的秩与它所含向量的个数相同.

每一向量组都与它的极大线性无关组等价.由等价的传递性可知，任意两个等价向量组的极大线性无关组也等价.所以，等价的向量组必有相同的秩.

含有非零向量的向量组一定有极大线性无关组，且任一个线性无关的部分向量都能扩充成一极大线性无关组.

规定:全部由零向量组成的向量组没有极大线性无关组.规定这样的向量组的秩为零.

四、向量组与方程组的联系

现在把上面的概念与方程组的解的关系进行联系，给定一个方程组

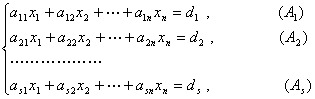
各个方程所对应的向量分别是

.设有另一个方程

它对应的向量为.则当且仅当，即方程(B)是方程 的线性组合.容易验证，方程组的解一定满足(B).进一步设方程组

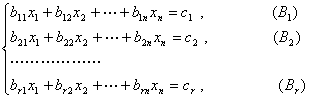
它的方程所对应的向量为.若可经 线性表出，则方程组的解是方程组 的解.

结论:当与等价时，两个方程组同解.

例5 （1）设线性无关，证明也线性无关；对个线性无关向量组，以上命题是否成立？

（2）当线性无关，证明也线性无关，当线性无关时，是否也线性无关？

例6 设在向量组中，且每个都不能表成它的前个向量的线性组合，证明线性无关.

  证明:反证.设相关,则有(其中不全为零)

设是最后一个非零的系数,则可以表成前个向量的线性组合…

    瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）