§1  消元法   <<返回

一. 线性方程组的初等变换

    1.基本概念

现在讨论一般线性方程组                    (1)

其中 称为线性方程组的系数， 称为常数项.( 与 不一定相等).系数 的 表示它在第 个方程， 表示它是 的系数.

方程组(1)的解的全体称为它的解集合.解方程组实际上就是找出它全部的解，或者说，求出它的解集合.如果两个方程组有相同的解集合，它们就称为同解的.

2.消元法解题之例

例:解方程组                         

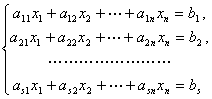
解:……求出方程组的解为（9，-1，-6）.

分析一下消元法，它实际上是反复地对方程组进行下列三种基本的变换：

1. 用一非零数乘某一方程；2. 把一个方程的倍数加到另一个方程；3. 互换两个方程.

二、线性方程组的解的情形

1.定义1 变换1，2，3称为线性方程组的初等变换.

2.结论:初等变换总是把方程组变成同解的方程组….

3.分析:利用初等变换来解一般的线性方程组.

对于方程组(1)，首先检查的系数.如果的系数全为零,…方程组(1)可以看作的方程组来解.如果的系数不全为零，那么利用初等变换3，可以设.利用初等变换2，分别把第一个方程的倍加到第个方程().于是方程组(1)就变成                       (3)

其中                    

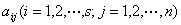
这样，解方程组(1)的问题就归结为解方程组

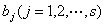                       (4)

的问题.显然(4)的一个解，代入(3)的第一个方程就定出的值，这就得出(3)的一个解；(3)的解显然都是(4)的解.这就是说，方程组(3)有解的充要条件为方程组(4)有解，而(3)与(1)是同解的，因之，方程组(1)有解的充要条件为方程组(4)有解.

对(4)再按上面的考虑进行变换，并且这样一步步作下去，最后就得到一个阶梯形方程组.不妨设所得的方程组为

                (5)

其中 .这时去掉它们也不影响(5)的解.而且(1)与(5)是同解的.

现在考虑(5)的解的情况.

如(5)中有方程，而.这时不管取什么值都不能使它成为等式.故(5)无解，因而(1)无解.

当是零或(5)中根本没有“0=0”的方程时，分两种情况：

1）.这时阶梯形方程组为

               (6)

其中.

由最后一个方程开始，的值就可以逐个地唯一决定了.在这个情形，方程组(6)也就是方程组(1)有唯一的解.

2）.这时阶梯形方程组为

其中.把它改写成

           (7)

由此可见，任给一组值，就唯一地定出的值，也就是定出方程组(7)的一个解.一般地，由(7)我们可以把通过表示出来，这样一组表达式称为方程组(1)的一般解，而称为一组自由未知量.

 例1 解线性方程组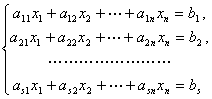      (结论:(9,-1,-6))

例2 解线性方程组

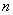               (结论:)

4.用消元法判断线性方程组的解的步骤:

（１）用初等变换化线性方程组为阶梯形，去掉最后的一些恒等式“0=0”(如果有).

（２）如果剩下的方程中最后的一个等式是零等于一非零的数，那么方程组无解，否则有解.

（３）有解时，如果阶梯形方程组中方程的个数等于未知量的个数，那么方程组有唯一的解；如果阶梯形方程组中方程的个数小于未知量的个数，那么方程组就有无穷多个解.

 5.齐次方程组的解的情形

定理1 在齐次线性方程组中，如果，那么它必有非零解.

例3 解线性方程组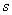   (结论:无解)

瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）