<<返回
                                     §8 拉普拉斯(Laplace)定理 行列式的乘法规则

一、拉普拉斯定理

1.定义9 在一个级行列式中任意选定行列()，位于这些行和列的交点上的个元素按照原来的次序组成一个级行列式，称为行列式的一个级子式.在中划去这行列后余下的元素按照原来的次序组成的级行列式称为级子式的余子式.

从定义立刻看出，也是的余子式.所以和可以称为的一对互余的子式.

例1 在四级行列式                     

中选定第一、三行，第二、四列得到一个二级子式,的余子式为 .

例2 在五级行列式            

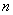
中和是一对互余的子式.

2.定义10 设的级子式在中所在的行、列指标分别是，则的余子式前面加上符号后称做的代数余子式.

3. 拉普拉斯定理

因为与位于行列式中不同的行和不同的列，所以有

引理 行列式的任一个子式与它的代数余子式的乘积中的每一项都是行列式的展开式中的一项，而且符号也一致.

证明:先讨论M位于的左上方的情形.结合行列式的定义.(注意逆序数的对应).

再证一般的情形.主要研究逆序数的变化.通过多次的对换化成前面的情形……

定理6(拉普拉斯定理) 设在行列式中任意取定了()个行.由这行元素所组成的一切级子式与它们的代数余子式的乘积的和等于行列式.

证明:(此定理可以看成行列式按行展开的推广)

设取定行后子式为，代数余子式分别为.定理要证

由引理,中每一项都是的一项且符号相同,而且各项无公共项下面的问题就是验证两边项数相同……

例3 利用拉普拉斯定理计算行列式

    (按第一、二行展开。结果：-7)

（从这个例子来看，利用拉普拉斯定理来计算行列式一般是不方便的.这个定理主要是理论方面的应用）.

二、行列式的乘积法则

定理7 两个级行列式           

和            

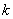
的乘积等于一个级行列式            ,

其中是的第行元素分别与的第列的对应元素乘积之和：

.

    证明:先构造一个行列式:                  

据拉普拉斯定理,按前n行展开得.再证D=C.对D做初等行变换,使变为0.此时行列式成为 再由拉普拉斯定理得到结论……

这个定理也称为行列式的乘法定理.它的意义到第四章§3中就完全清楚了.

   瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）