§7 克拉默(Cramer)法则   <<返回

一、回顾解线性方程组的情形．．．

二、克拉默法则

现在应用行列式解决线性方程组的问题.这里只考虑方程个数与未知量个数相等的情形.

定理4(克拉默法则)如果线性方程组

                        (1)

的系数矩阵 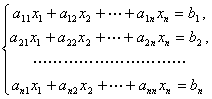                                   (2)

的行列式那么线性方程组(1)有解，并且解是唯一的，解可以通过系数表为

,                 (3)

其中是把矩阵中第列换成常数项所成的矩阵的行列式，即

      (4)

证明:定理中包含着三个结论：1）方程组有解；2）解是唯一的；3）解由公式(3)给出.这三个结论是有联系的，因此证明的步骤是：1. 把代入方程组，验证它确是解.2. 假如方程组有解，证明它的解必由公式(3)给出.

例1 解方程组

(结论:有唯一解:)

注:定理4所讨论的只是系数矩阵的行列式不为零的方程组，它只能应用于这种方程组；至于方程组的系数行列式为零的情形，将在下一章的一般情形中一并讨论.

三、齐次线性方程组的解

１．常数项全为零的线性方程组称为齐次线性方程组.

２．显然齐次方程组总是有解的，因为就是一个解，它称为零解.

（对于齐次线性方程组，我们关心的问题常常是，它除了零解以外，还有没有其它解．．．）

３．定理5 如齐次线性方程组                  (10)

的系数矩阵的行列式，那么它只有零解.换句话说，如果(10)有非零解，那么必有.

例2 求在什么条件下，方程组有非零解.

（克拉默法则的意义．．．）    (结论:时)

  瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）