§6  行列式按一行(列) 展开    <<返回               

一、分析：行列式的“降阶”

在行列式的定义中， 级行列式的项可以分成组，第一组的项都含有，第二组的项都含有等等.再分别把行的元素提出来，就有

         (1)

其中代表那些含有的项在提出公因子之后的代数和.从以上讨论可知，中不再含有第行的元素，也就是全与行列式中第行的元素无关.

二、余子式与代数余子式

１．定义7 在行列式det()中划去元素所在的第行与第列，剩下的个元素按原来的排法构成一个级行列式

              (2)

称为元素的余子式，记作

2.结论:                   .                         (3)

证明:先证明级行列式与级行列式的关系，

. （4）

再用对换变成一般的情形……

3．定义8 上面所谈到的称为元素的代数余子式.

     这就是说，在行列式中，一行的元素与另一行相应元素的代数余子式的乘积之和为零.

例：三级行列式可以通过二级行列式表示：

.             (5)

三、行列式按行（或列）展开

１．定理3 设             

则　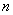　　　　　　                 (6)

                 (7)

   证明:根据行列式的定义、性质和“分析”…

注：在计算数字行列式时，往往要结合其它方法同用才简便．．．但这两个公式在理论上是重要的.

例1 计算行列式      (结论:-1080)

例2 行列式                    (8)

称为级的范德蒙德(Vandermonde)行列式.证明对任意的 

d=.

由这个知范德蒙德行列式为零的充要条件是这个数中至少有两个相等.

例3 证明

    证明:法一:用数学归纳法结合行列式按行列展开(按第一行展开)……

         法二:根据行列式的定义……

　　２．用定理３求行列式的注意事项．．．

       瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）