<<返回               
                                               §5  行列式的计算

　　一、引例

在§3我们看到，一个上三角形行列式就等于它主对角线上元素的乘积(由行列式的性质) 下面把任意的级行列式化为上三角形行列式来计算.

　　二、矩阵的概念

１．定义5 由个数排成的行列的表

                         (1)

称为一个矩阵.

　　２．相关概念

数,称为矩阵(1)的元素，称为元素的行指标，称为列指标.当一个矩阵的元素全是某一数域中的数时，它就称为这一数域上的矩阵.

矩阵也称为级方阵.一个级方阵         

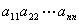
定义一个级行列式                 

称为方阵的行列式，记作.

　　３．矩阵与行列式的关系

　　（１）不同：矩阵是数表；行列式是“方型”数表的一种算法，其值为数。

　　（２）联系：行列式中的数表为一种特殊的矩阵：方阵。

　　三、矩阵的初等变换

１．定义6 所谓数域上矩阵的初等行(列)变换是指下列三种变换：

1）以中一个非零的数乘矩阵的某一行(列)；

2）把矩阵的某一行的倍加到另一行(列)，这里是中任意一个数；

3) 互换矩阵中两行(列)的位置.

２．矩阵的初等行变换与初等列变换统称为初等变换.

一般说来，一个矩阵经过初等行变换后，就变成了另一个矩阵.当矩阵经过初等行变换变成矩阵时，我们写成

若矩阵的任一行从第一个元素起至该行的第一个非零元素所在的下方全为零，则称这样的矩阵为行阶梯形矩阵.可以证明，任一矩阵经过一系列初等行变换总能变成阶梯形矩阵.

四、用矩阵的初等变换求行列式的值

１．方法：一个级行列式可看成是由一个级方阵决定的，对于矩阵可以作初等行变换，每个方阵总可以经过一系列的初等行变换变成阶梯形方阵 .显然，阶梯形方阵的行  列式都是上三角形的，因此是容易计算的.

例  计算          (结论:312)

２．优点：（１）对比较大的时候，这个方法简便。（２）此法可以用电子计算机计算.

注：为了计算行列式，也可以对矩阵进行初等列变换…

  瀚海代数精品课程网资源  （需要原word文档请联系：nchy_zouzij@163.com）