一.填空题(每空3分,共24分)
1.在![]() 中,基
中,基![]() 到基
到基![]()
![]() 的过渡矩阵是
的过渡矩阵是
2.数域P上全体![]() 阶方阵对于矩阵的加法和数乘构成
维向量空间。
阶方阵对于矩阵的加法和数乘构成
维向量空间。
3.设数域P上三维列向量空间![]() 的线性变换
的线性变换![]() 在基
在基![]() 下的矩阵是
下的矩阵是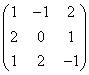 ,则
,则![]() 在基
在基![]() 下的矩阵是
。
下的矩阵是
。
4.![]() 是
是![]() 维向量空间
维向量空间![]() 的子空间,关于子空间的维数公式是
的子空间,关于子空间的维数公式是![]()
。
5.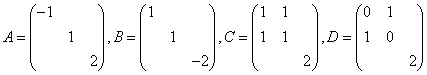 是
是![]() 上3阶方阵,则在
上3阶方阵,则在![]() 中,
与
中,
与![]() 正交相似(即相似变换是正交变换)。
正交相似(即相似变换是正交变换)。
6.在![]() 中,定义内积为标准内积,则向量
中,定义内积为标准内积,则向量![]() 的夹角是
,距离是
。
的夹角是
,距离是
。
7.![]() 中,与矩阵
中,与矩阵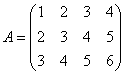 的每个行向量都正交的全体向量所构成的子空间
的每个行向量都正交的全体向量所构成的子空间![]() 的维数为
。
的维数为
。
二、(12分)在![]() 中,求基(1)
中,求基(1)![]() 到基(2)
到基(2)![]() 的过渡矩阵。判断它是否正交阵,并说明原因。
的过渡矩阵。判断它是否正交阵,并说明原因。
三、(12分)![]() (数域P上所有次数不大于3的多项式与零构成的线性空间)的线性变换如下
(数域P上所有次数不大于3的多项式与零构成的线性空间)的线性变换如下
![]()
求它在基![]() 下对应的矩阵。并求其子空间
下对应的矩阵。并求其子空间![]() 的象空间。
的象空间。
四、(10分)若矩阵A的不变因子为1,1,1,1,![]()
![]() ,求其若当标准型。
,求其若当标准型。
五、(10分)欧氏空间![]() 定义的内积为
定义的内积为
![]()
求其在基(1,0,0),(0,1,0),(0,0,1)下的度量矩阵。并依此度量矩阵求向量(1,1,1)的长度。
六.(12分)判断线性空间![]() (实数与
(实数与![]() 上2阶方阵的全体)下的变换
上2阶方阵的全体)下的变换
![]() 为
为![]() 中固定的矩阵)
中固定的矩阵)
是否线性变换。它是否到自身的同构?
七.(10分)证明:正交变换不改变向量的长度与俩向量的夹角。
八.(10分)欧氏空间![]() 上的变换
上的变换![]() 定义为
定义为
![]()
证明:![]() 是线性变换,且为对称变换。
是线性变换,且为对称变换。
--瀚海网原创资源--