一、填空（30分）
1.在欧氏空间R3（R为实数集，内积为常见的内积）中向量（1，2，2）的长度为 .
2．若V1与V2 为8维线性空间V的子空间。且维数分别为2与3 .当
时，
的维数为
.
3.
设
是向量空间V的一组基，线性变换s在此基下对应的矩阵为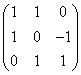
，则s在基
下对应的矩阵为 .
4．设矩阵的若当标准型为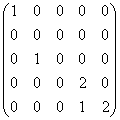
，则此矩阵的初等因子为
.
5.
设三阶方阵A的三个特征值为1，1，2，则
= .
6．正交的向量组必为
向量组。
7.V为线性空间，A为V上的可逆的线性变换，W为V的A-子空间，则AW= .
8.设A与B均为实数域上的n阶方阵,A与B相似的充分必要条件是它们的特征矩阵
9.标准正交基中的每一个向量的长度为
。
10.正交变换将标准正交基变成
。
二、（15分）设
是3维线性空间V的一组基, 线性变换A在这组基下的矩阵为
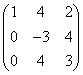
1.
求A在基
下的矩阵；
2.
求A的特征值与特征向量.
三（10分）设V是n维欧氏空间，a ¹ o是V中一个固定向量.证明：
1.
U = { b | ( b, a ) =o, bÎV }是V的一个子空间；
2.
U的维数等于n -1.
四（15分）设A是线性空间V的可逆线性变换，则
1)
A的特征值必不为0；
2)
如果l是A的特征值，那么
是A2的特征值。
五．（15分）在线性空间R4中，求向量(1,1,1,1)在基
A: (1,0,0,0) ，(1,1,0,0)，(1,0,1,0)， (1,0,0,1)
下的坐标。并求基A到B: (2,0,0,0)，(0,2,0,0)， (0,0,2,0)， (0,0,0,2)
的过渡矩阵。
六．（15分）求二次型
在正交变换下的标准型
--瀚海网原创资源--
http://hanhai.org