一、选择题（30分，每题3分）
1、 若A,B 均为n阶方阵，A,B有相同的特征值且均非零，则 （ ）
(A)A,B相似；（B）A,B合同； （C）A,B等价； （D）A,B有相同的若尔当标准型。
2、若矩阵P与Q相似，下列说法错误的是 （ ）
（A）P与Q有相同的特征值；
（B）P与Q有相同的对角形；
（C）P 与Q可以看作同一线性变换在不同基下的矩阵；
（D）P与 Q对应的行列式的值相同。
3、Q为n阶方阵，其秩为r.A
为一个
上的线性变换（
）.A的核的维数为
（ ）
（A）r维； (B) n维； (C) n-r维； (D)0维。
4、数域P中的矩阵一定能通过相似变换化成对角形的是 （ ）
(A)矩阵的特征多项式不能在P中完全分解；
(B)矩阵的特征多项式可以在P中完全分解；
(C)矩阵的初等因子全为一次式；
(D)矩阵仅有一个初等因子。
5、设矩阵A的不变因子为1,1, 1，1，
，则它的初等因子为 （ ）
(A)1,1, 1，1，
；
(B)；
(C)
；
(D)
.
6、若向量空间R4 中，两向量分别为(1,0,1,0)，（-2,2,1,1），则其夹角为 （ ）
(A)
(B) 
(C) 
(D) 
7、关于欧几里得空间，下列说法正确的是 （ ）
(A)任一线性空间都能适当定义内积成为欧几里得空间；
(B)欧几里得空间未必是线性空间；
(C)欧几里得空间必为实数域上的线性空间；
(D)欧几里得空间可以为有理数域上的线性空间。
8、下列矩阵不一定是正交阵的是 （ ）
(A)正交变换在任一组标准正交基下的矩阵；
(B)其转置矩阵为其逆矩阵的方阵；
(C)其列向量组为单位向量且构成的正交向量组的方阵；
(D)欧几里得空间在某基下的度量矩阵。
9、实数域上的多项式
为 （
）
(A)可约的非本原多项式；
(B)可约的本原多项式；
(C)不可约的本原多项式；
(D)不可约的非本原多项式。
10、设f为R3到C的函数，下列是线性函数的是 （ ）
(A)
；
(B)
；
(C)
；
(D)
.
二、计算题（54分，每题9分）
1、 在R4(加法与数乘为常见的加法与数乘)中求由基
到基
的过渡矩阵，并求向量
在基
下的坐标.
2、在
（P为数域）中，A定义如下：
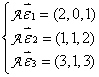其中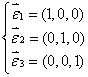
求A在基
下的矩阵，并求A的值域与核。
3、求相似变换，将下列矩阵化成对角形：
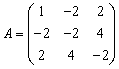
4、若５级矩阵A的若当标准形为
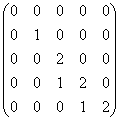
求其特征值、初等因子与不变因子。
5．在线性空间R[x]4（所有次数小于4的实数域R上的多项式的全体）中定义内积为
.验证R[x]4为欧氏空间，并且
是它的一组标准正交基。
6．设在欧氏空间R3中(内积按通常定义)有一组基
求此基的度量矩阵，并用此度量矩阵求
的长度。
三、证明题（16分）
1、(8分)证明：数域P上的2阶方阵的全体关于矩阵的加法与矩阵的数乘作成线性空间，并且其维数为4.
2、（8分）证明：设1，2，-1，-1为数域P上的4维线性空间V上的线性变换A的特征值。则：A的值域为V,且1/2为A -1 的一个特征值。
--瀚海网原创资源--
http://hanhai.org