一、填空题（共24分）
1．实对称矩阵的属于不同特征根的特征向量是彼此
。
2．若
是线性空间
的一个基，则满足条件
（1）是
；
（2）对中任意向量
，有
.
3．设
是向量空间的一个基，由该基到
的过渡矩阵为___________________。
4. 设
为线性变换，为欧氏空间，若
都有
，则
为
变换。
5. 设矩阵
是
阶零矩阵，则的个特征值是 。
6．设矩阵A的不变因子为
,则其初等因子为
。
7．多项式
在实数域
上的标准分解为 。
二、（10分）设
是
的一个基，而
是另一组基，求由
到
的过渡矩阵，并求向量
在下的坐标。
三．（10分）求多项式
的有理根。
四．（20分）判断
（1）
中的子集
是否为的子空间。
（2）
中的子集
是否为的子空间。
五、（10分）求矩阵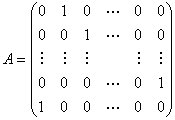
的若尔当标准形.
六.(10分) 设A是任意实对称矩阵，证明：存在实数t，使得tE+A是正定矩阵。（E是单位矩阵）
七．(8分)证明:一个正交变换的逆变换还是一个正交变换。
八．（8分）证明： 设
是三维欧氏空间的一个标准正交基，试证：
也是的一个标准正交基。
--瀚海网原创资源--
http://hanhai.org