高等代数1试卷4A 答案 返回

一、选择题 (每题3分,共30分)

1．下列哪一个排列是四级偶排列 （ ）

(A)1324 (B)4123 (C) 4132 (D)2341

2.下列数集中关于数的四则运算有几个是数域 ( )

(A)4　 　　(B)3 　　 (C)2 　(D)1

3．设n阶方阵A与B只是第j列不同，则 |A+B|等于 ( )

(A)2 ^n-1 (|A|+|B|) (B)2 (|A|+|B|) (C)2 ⁿ (|A|+|B|) (D)|A|+|B|

4.二次型为 （ ）

(A)半正定的 （B）正定的 (C)不定的 (D)不能确定

5. 设A是n阶可逆矩阵(n³2)，A*是A的伴随矩阵，则下列哪一个必成立 ( )

(A)(A*)*=|A|^n-1A (B)(A*)*=|A|^n-2A (C) (A*)*=|A|^n+1A (D) (A*)*=|A|^n+2A

6. 设矩阵A=，A^*是A的伴随矩阵，则A^*中位于第一行第二列的元素是 ( )

(A)-6 (B) 6 (C)2 (D) -2

7. ( )

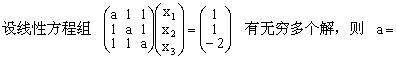(A) 3 (B) 0 (C) -2 (D) -3

8. 若A是n阶可逆矩阵，则下列命题中错误的是 ( )

(A) 必可逆 (B) A² 必可逆

(C) -2A必可逆 (D) A+E 必可逆

9.多项式为 ( )

(A)不可约的本原多项式 (B)可约的本原多项式

(C)不可约的非本原多项式 (D)可约的非本原多项式

10. 已知矩阵

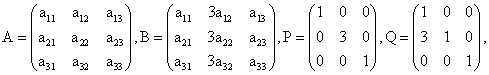
则 B= ( )

(A) AP (B) QA (C) PA (D) AQ

二、求解（12分，每题6分）

1．求下列行列式的值

2．求矩阵的逆

三、（12分）讨论a,b取什么值时下列线性方程组无解，有唯一解，有无穷多解？并在有无穷多解时求出其通解。

四、（10分）求向量组=(0,0,2,3), =(1,2,3,4)，=(1,2,1,1)，=(1,0,1,0)的一个极大线性无关组。

五．（10分）求下列实二次型的标准形，并指出其正惯性指数和负惯性指数。

f(x₁, x₂,x₃)= x₁²+4x₁ x₂+2 x₁x₃+4x₂²+4 x₂ x₃+3x₃²

六．(10分)(1) 叙述艾森斯坦判别法；

（2）设f(x)=x⁵+5x+1，判别 f(x) 在有理数域上是否不可约？

七.证明题（16分）

1．(6分)设A为n阶反对称矩阵，即A= -A，证明：当n为奇数时，|A|=0.

2．(10分)设 a 是非齐次线性方程组AX=的一个特解，是其导出组AX=的一个

基础解系。令 . 试证明：是线性方程组AX=的全部解向量的一个极大无关组。

瀚海网出品

http://www.hanhai.org