一.选择题(每题3分,共24分)
1.
多项式![]() ,则
( )
,则
( )
(A)![]() 的次数为零当且仅当
的次数为零当且仅当![]() 等于零;(B)
等于零;(B)![]() 的次数等于
的次数等于![]() ;
;
(C)![]() 的次数等于
的次数等于![]() 次数之和;(D)
次数之和;(D)![]() 的次数小于
的次数小于![]() 次数之和。
次数之和。
2. 下列集合可以构成数域的是 ( )
(A)整数集; (B)正实数集; (C) 实数上的所有多项式; (D) ![]()
3.设非零的![]() 矩阵
矩阵![]() 的行列式为零, 则
( )
的行列式为零, 则
( )
(A)![]() 中至少有一行(列)元素全为零或至少有两行(列)元素对应成比例关系;
中至少有一行(列)元素全为零或至少有两行(列)元素对应成比例关系;
(B)齐次线性方程组![]() 有非零解;
有非零解;
(C)![]() 的行向量组和列向量组不可能都是线性相关的;
的行向量组和列向量组不可能都是线性相关的;
(D)线性方程组![]() 有无穷多解.
有无穷多解.
4.设![]() , 两个
, 两个![]() 维向量组
维向量组![]() (1) 和
(1) 和![]() (2), 下述正确的是 ( )
(2), 下述正确的是 ( )
(A)若(1)可由(2)线性表出, 则(1)线性相关;
(B)若(1)可由(2)线性表出, 则(1)未必线性相关;
(C)若(1)可由(2)线性表出, 则当(2)线性无关时, (1)线性无关;
(D)若(1)可由(2)线性表出, 则仅当(2)线性相关时, (1)线性相关.
5.设线性方程组![]() 与线性方程组
与线性方程组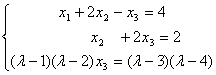 同解.则线性方程组
同解.则线性方程组![]() 无解的充分且必要条件是( )
无解的充分且必要条件是( )
(A) ![]() 或
或![]() ; (B)
; (B) ![]() 或
或![]() ; (C)
; (C) ![]() 或
或![]() ;(D)
;(D) ![]() 或
或![]() .
.
6.设矩阵![]() 为
为![]() 的,
的,![]() 为
为![]() 的且
的且![]() ,下述正确的是 (
)
,下述正确的是 (
)
(A)当B不满秩时,必有C=O;
(B)当B满秩时,未必有C=O;
(C)当B不满秩时,必有C![]() O;
O;
(D) 当B满秩时,必有C=O.
7.关于二次型,有下列四种说法:
(1)二次型的标准型存在且唯一;
(2)复数域上的二次型的标准型对应的矩阵是单位阵;
(3)正定的二次型是满秩的;
(4) 二次型的正惯性指数与负惯性指数的和为此二次型的秩.
上述说法中,正确的是 ( )
(A) (1)和(2)
(B) (3)和(4) (C) (2)和(3) (D)(1)和(4)
8.如果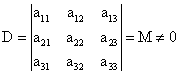 ,
, 那么
那么![]() ( )
( )
(A)
二.计算题(每题10分,共40分)
1.设![]() ,
, ![]() ,用
,用![]() 除以
除以![]() 做带余除法。
做带余除法。
2.求解矩阵方程![]() ,其中
,其中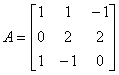 ,
, 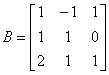 .
.
3.![]() 取什么值时, 线性方程组
取什么值时, 线性方程组
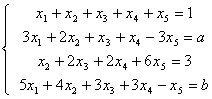 无解?有解?有解时,求出由基础解系表示的全部解.
无解?有解?有解时,求出由基础解系表示的全部解.
4.求下列矩阵的秩和一个最高阶非零子式.

三.判断题(16分)
分别判断下列两组向量组是否线性相关,若相关,则求其最大无关组;若无关,则增加一个向量使之仍无关.
(1)![]()
(2) ![]()
四.证明题(每题10分,共20分)
1.向量组![]() 与
与![]() 等价,
等价, ![]() 的秩为m,则
的秩为m,则
![]()
的秩也为m.
2.设A,B是两个n 阶方阵,证明:![]() 同解。
同解。
http://hanhai.org