一. 填空题(21分,每空3分)
1.已知![]() ,其中
,其中![]() ,则
,则![]() _________。
_________。
2.设![]() 都是
都是![]() 阶可逆阵,
阶可逆阵,![]() ,则
,则![]() _________。
_________。
3.设![]() 是一个
是一个![]() 矩阵,
矩阵,![]() 是一个
是一个![]() 矩阵,那么
矩阵,那么![]() 是一个________阶矩阵,它的第i行第j列元素为________。
是一个________阶矩阵,它的第i行第j列元素为________。
4.设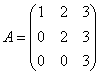 ,则A的秩为
。
,则A的秩为
。
5.设![]() ,
,![]() 都是可逆矩阵,矩阵C=AB的逆矩阵可表示为________。
都是可逆矩阵,矩阵C=AB的逆矩阵可表示为________。
6.设方阵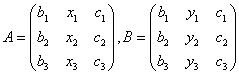 ,且
,且![]() ,则行列式
,则行列式![]() ________。
________。
二.选择题(24分,每题3分)
1.![]() 是
是![]() 矩阵,
矩阵,![]() 是
是![]() 矩阵,若
矩阵,若![]() 的第
的第![]() 列元素全为零,则下列结论正确的是( )
列元素全为零,则下列结论正确的是( )
(A)![]() 的第
的第![]() 列元素全等于零 (B)
列元素全等于零 (B)![]() 的第
的第![]() 行元素不全等于零
行元素不全等于零
(C)![]() 的第
的第![]() 列元素全等于零 (D)
列元素全等于零 (D)![]() 的第
的第![]() 行元素不全等于零
行元素不全等于零
2.![]() 均为
均为![]() 阶矩阵,
阶矩阵,![]() 为
为![]() 阶单位矩阵,若
阶单位矩阵,若![]() ,则有
( )
,则有
( )
(A) ![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
3.设![]() 是5阶方阵,且
是5阶方阵,且![]() ,则
,则![]() =
( )
=
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
4.设![]() 是
是![]() 的伴随阵,则
的伴随阵,则![]() 为
( )
为
( )
(A)E (B)|A| (C)|A|E (D) 以上均不对![]()
![]()
5.设![]() ,
,![]() 是两个
是两个![]() 矩阵,
矩阵,![]() 是n阶方阵,那么
( )
是n阶方阵,那么
( )
(A) ![]() (B)
(B)
![]()
(C) ![]() (D)
(D) ![]()
6.设![]() ,则
,则![]() ( )
( )
(A) 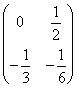 (B)
(B) 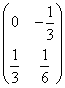 (C)
(C) 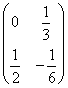 (D)
(D) 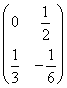
7.若![]() 可逆,则
可逆,则![]() 的解是
的解是![]() = ( )
= ( )
(A) 不存在 (B) ![]() (C)
(C) ![]() (D)
(D) ![]()
8.设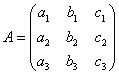 ,若
,若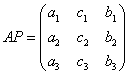 ,则P=
( )
,则P=
( )
(A) 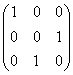 (B)
(B) 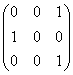
(C) 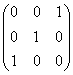 (D)
(D) 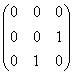
三.(8分)解矩阵方程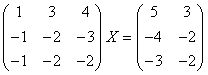
四.(5分)计算行列式

五(10分)求线性方程组
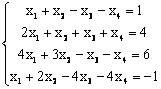
的通解。
六(8分)判别下列二次型的正定性:
![]()
七.(6分)设![]() 是
是![]() 阶可逆阵,调换
阶可逆阵,调换![]() 的第
的第![]() 列与第
列与第![]() 列得到矩阵
列得到矩阵![]() .求证
.求证![]() 可逆。
可逆。
八.(8分) 证明:若向量组![]() 的秩为3,且此向量组与向量组
的秩为3,且此向量组与向量组
![]() 等价,则向量组
等价,则向量组![]() 的秩为3.
的秩为3.
九 (10分)证明:设![]() 是数域
是数域![]() 上的不可约多项式,
则
上的不可约多项式,
则![]() 在复数域上没有重根.
此命题的逆命题是否成立? 为什么?
在复数域上没有重根.
此命题的逆命题是否成立? 为什么?
瀚海网出品
http://hanhai.org