一、
填空题（每小题3分，共24分）
1．已知多项式f(x)＝d(x) f1(x)，g(x)＝d(x) g1(x) 且（f(x)，g(x)）＝d(x)，则（f1(x)，g1(x)）＝
.
2．当m，p，q适合 条件时，有
|
.
3．设A＝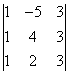
，则A31＋A32＋A33＝
.
4．设A为3级方阵，
＝
，则
＝ .
5．已知向量组α1＝（1,4,3），α2＝（-2,3,1），α3＝（-1，k，4）线性相关，则参数k＝ .
6．设A＝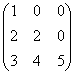
，A*是A的伴随矩阵，则(A*)
＝
.
7．n级排列23…n1的逆序数为 .
8．设
为分块矩阵,E为单位矩阵.且
可逆.则
.
二、判断题（对的打√，错的打×，每小题2分，共12分）
1．若d(x)＝u(x)
f(x)＋v(x) g(x) 则d(x)|f(x)且d(x)|g(x) .
( )
2．设A为n阶方阵，若|A|<0，则A为可逆矩阵。
( )
3．若向量组α1,α2,...，αm(m≥2)中每个向量都不能由其余向量的线性表示，则此向量组线性无关。 ( )
4．若A、B为n阶矩阵，且A≠O,B≠O,则有|AB|≠0. ( )
5．正定的二次型的矩阵合同于单位矩阵。
( )
6.设A,B均为对称阵，则AB为对称阵。
( )
三、计算题（每小题8分，共48分）
1．计算行列式D＝
，i＝1,2，...，n.
2．求下列向量组的秩和一个极大无关组，并将α1，α2拓展成整个向量组的极大无关组。
α1＝（1,0，－1，0），α2＝（－1，2,0，1），α3＝（－1, 4，－1，2），
α4＝（0, 0，5，5），α5＝（0, 1，1，2）.
3．已知A＝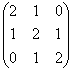
，B＝
，求矩阵X使之满足AX＝X+B.
4．求t的值,使下列方程组有解,并求其通解。
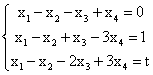
5．设
, 
,
(1)在复数域上求它们的公共根; (2)求它们在实数域上的标准分解式。
6．用非退化线性替换化下列二次型为标准型（要求写出线性替换）。
四、证明题（每小题8分，共16分）
1、 设A为n（n≥2）级方阵，A＊为A的伴随矩阵，证明：
(1)| A＊|＝|A|n－1.
(2)若A可逆.则| A-1|＝|A|－1.
2、已知向量组α1，α2，…，αs为某齐次线性方程组的一个基础解系，且
β1＝α1，
β2＝α1＋α2，
β3＝α1＋α2＋α3，
………
βs＝α1＋α2＋…＋αs，
证明：向量组β1，β2，……，βs也为该齐次线性方程组的一个基础解系。