第九次习题课
内容:第七章
重点:向量的概念、坐标表示与各类运算、
空间直线、平面的方程.
难点:向量的向量积、空间曲面.
专题1 有关向量的各类概念的分类与联系
1.
向量的基本概念及其属性:
向量的模(大小),向量的方向,两向量的夹角(特殊:平行,垂直)。
2.向量的运算:
1)加法 2)数乘 3)数量积 4)向量积
3.向量的坐标表示:
1)预备:数轴(一维、二维、三维),笛卡尔坐标系。点与坐标的对应。投影。
2)向径与向量的表示:
模的表示;方向的表示---方向角;向量夹角的表示;向量运算的表示。
例1
在三维笛卡尔坐标系中,有一个平行
四边形ABCD,已知A、B、C的坐标:
A(1,0,1) B(3,1,2) C(2,2,0)
1)
求D点的坐标。
2)
求![]() 、
、![]() 的夹角。
的夹角。
3)
求平行四边形ABCD的面积。
4)
验证ABCD的两个对角线垂直。
5)
将平行四边形平行移动,使得B点移至
原点,求另外三点移动后的坐标。
答案 1)![]() =
=![]() +
+![]() ={-3,0,-3},D(0,1,-1)
={-3,0,-3},D(0,1,-1)
2)arccos(1/2)=![]()
3) |![]()
![]()
![]() |=|
|=|![]() ||
||![]() |sin
|sin![]() =3
=3![]()
4) ![]() ={-3,0,-3},
={-3,0,-3},![]() {1,2,-1},内积。
{1,2,-1},内积。
5)原![]() ={-1,1,-2},C移动到(-1,1,-2)
={-1,1,-2},C移动到(-1,1,-2)
原![]() ={-2.-1,-1},A移动到(-2,-1,-1)
={-2.-1,-1},A移动到(-2,-1,-1)
原![]() ={-3,0,-3},D移动到(-3,0,-3)
={-3,0,-3},D移动到(-3,0,-3)
例2
A(1,1,2),B(3,3,-2),求yOz
面上点C,在AB的垂直平分线上且与AB距
离为![]() 。
。
提示:与A,B两点距离相等。(答案:(0,2,-1)
专题2 向量的运算
一、线性运算.
1.加法; 2.数乘。
例3:设![]()
![]() ,试用
,试用![]() 表示
表示![]()
(答案:![]() )
)
二.非线性运算。
1.内积:![]()
2.外积:![]() 方向右手系。
方向右手系。
3.可解决的问题:
1) 共线问题与共面问题;
2) 求面积问题;
3)证明题(如证明不等式)。
例4:设点A,B,C的向径分别为
![]() 试证明A,B,C三点共线。
试证明A,B,C三点共线。
(提示:![]() 成比例。)
成比例。)
例5:直线L通过点A(-2,1,3)和B(0,-1,2),求点C(0,2,1)到直线L的距离。
(答案: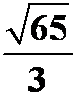 )
)
提示:1)利用外积; 2)利用内积。
例6: 试用向量证明不等式
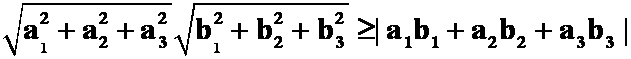 (提示:分别表示向量的长度与内积。)
(提示:分别表示向量的长度与内积。)
专题:空间直线、平面以及向量
一、空间直线
一般方程: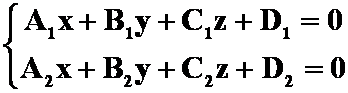
对称式方程:
点向式方程: 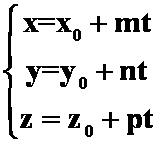
二.平面
点法式:
![]()
一般方程:![]()
例7:求过直线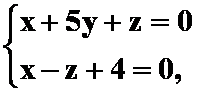 且与平面
且与平面
![]() 成
成![]() 角的平面方程。
角的平面方程。
(答案:![]() )
)
三、用向量及其运算解决平面与直线的问题
1.求平面以及直线的方程。
2.求线与线、线与面、面与面的夹角。
3.求点到平面的距离、点到直线的距离。
4.直线共面,平面共线等问题。
例8:求直线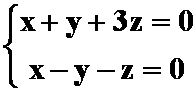 与平面
与平面![]() 间的夹角。(答案:
间的夹角。(答案: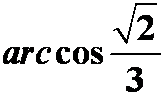 )
)
例9:证明:三个平面![]() ,
,![]() ,
,![]() 共线。
共线。
(提示:求平面系,简单。)
例10:求点P(3,-1,2)到直线
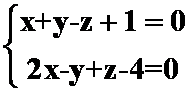
的距离。(答案: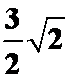 )
)
提示:求垂足,过此点作垂直两平面的平面即可。
思考:若直线是对称型怎么办?
如:求点P(3,-1,2)到直线
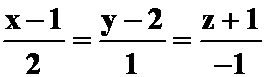
的距离。
(提示:有两种方法,前面例题中有一个向量的方法,还可以作垂直直线的平面。)
例11:求与直线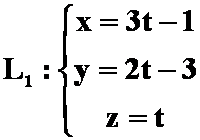 与直线
与直线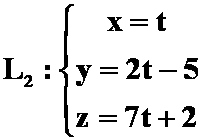 垂直且相交的直线方程。
垂直且相交的直线方程。
(答案: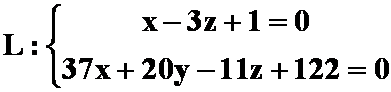 )
)
提示:所求直线的方向向量用![]() 的方向向量的外积求得。然后据
的方向向量的外积求得。然后据![]() ;
;![]() 各在一个平面上……
各在一个平面上……
注:由此可以得到启发,在没有规定的情况下,求直线(平面)的方程的型式可灵活。
专题:空间曲线、曲面
一、曲面
曲面的一般方程:F(x,y,z)=0
常用到的二次曲面:
截痕法确定曲面形状的要点:
1)
确定x,y,z的范围。
2)
确定主要的三个截面:x=0,y=0,z=0
的形状。
3)确定x,y,z变化时截痕的变化
4)确定特殊的部分(如边界、邻接线)的形状。
二、空间曲线
一般方程: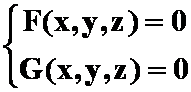
参数方程: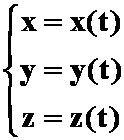
例12:说出下列方程表示的曲面
1)![]() 2)
2)![]()
3)xyz=0 4)![]()
5)![]() 6)
6)![]()
(答案:
1)
双曲柱面;2)锥面;
3)三个坐标平面;
4)双叶双曲面(或旋转双曲面);
5)旋转抛物面; 6)椭球。)
补充题:
选择题:
1.非零向量![]() 平行且同向,则下列式子中不正确的个数是
( )
平行且同向,则下列式子中不正确的个数是
( )
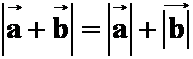 ;
;
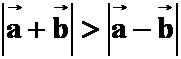 ;
;
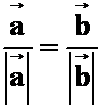 ;
; 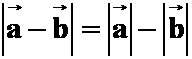 ;
;
A. ![]() ; B.
; B. ![]() ; C.
; C. ![]() ; D.
; D. ![]() ;
;
解:第四式不成立,当![]() 方向不同时,等式不成立。选B
方向不同时,等式不成立。选B
2.下列说法正确的是
( )
1)任何向量都有确定的大小和方向;
2)任何向量除以它自己的模都是单位向量;
3)![]() ,
,![]() 为非零向量且
为非零向量且![]() ,则
,则![]() 与
与![]() 平行;
平行;
4)只有模为![]() 的向量才是零向量;
的向量才是零向量;
A.
1)
2); B. 2) 3); C. 2) 4); D. 3) 4);
解1)零向量没有规定的方向
2)零向量不可以除自己的模。
选 D
3.已知![]() ,
,![]() ,则与
,则与![]() 平行的单位向量为
( )
平行的单位向量为
( )
A. 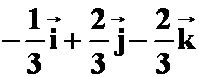 ;
;
B. 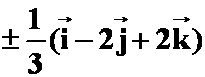 ;
;
C. 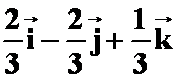 ;
;
D. 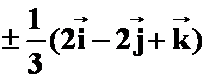 ;
;
解:
![]()
只有![]() 答案与之是平行的
答案与之是平行的
4.已知点![]() 和
和![]() ,则向量
,则向量![]() 的方向角
的方向角![]() 分别为 ( )
分别为 ( )
A.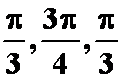 ; B.
; B. 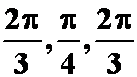 ;
;
C.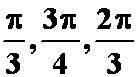 ;
D.
;
D. 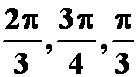 ;
;
解 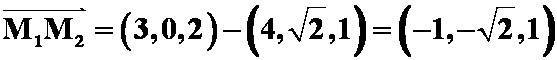

同理 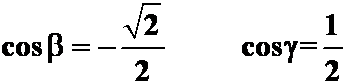
则夹角![]() 分别为
分别为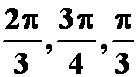
答案D
5. 设![]() 是单位向量,且
是单位向量,且![]() ,则
,则![]() ( )。
( )。
A. ![]() ; B.
; B. ![]() ; C.
; C. ![]() ; D.
; D. ![]() ;
;
解: 由![]() ,则有
,则有
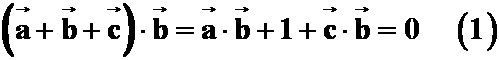
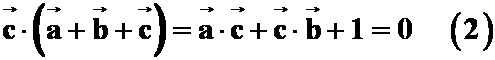
由![]() 有
有![]() 再
再
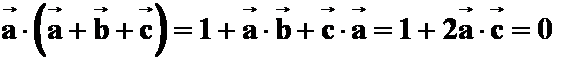 即得
即得![]()
![]() 选B
选B
6.下列曲线中,绕坐标轴旋转可以得到相同曲面的曲线是()。
1)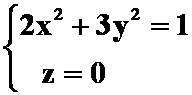 ; 2)
; 2)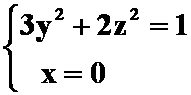 ;
;
3)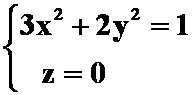
A.1) 2); B. 1) 3); C. 2) 3); D. 1) 2) 3);
解 ![]() 1)绕
1)绕![]() 轴旋转得
轴旋转得
![]()
2)绕![]() 轴旋转得
轴旋转得
![]()
![]() 选
选![]()
7.两平面![]() 的夹角为
( )。
的夹角为
( )。
A.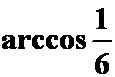 ; B.
; B. ![]() ; C.
; C. 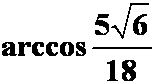 ; D.
; D. ![]() ;
;
解: 选C
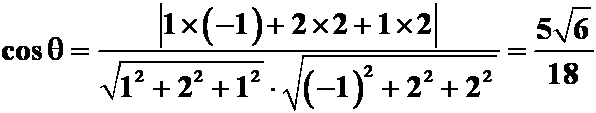 8.若两直线
8.若两直线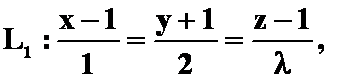
 相交,则
相交,则![]() ( )
( )
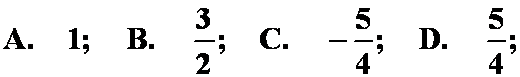
解: 设
得![]() 代入
代入![]()
得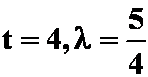 选D
选D
补充习题:
1. 设![]() 是单位向量,且
是单位向量,且![]() ,则
,则![]() ( )。
( )。
A. ![]() ; B.
; B. ![]() ; C.
; C. ![]() ; D.
; D. ![]() ;
;
解: 由![]() ,则有
,则有
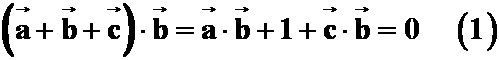
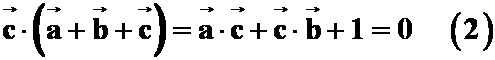
由![]() 有
有![]() 再
再
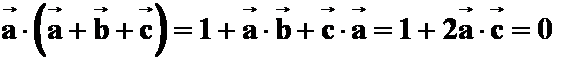 即得
即得![]()
![]() 选B
选B
2.下列曲线中,绕坐标轴旋转可以得到相同曲面的曲线是()。
1)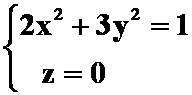 ; 2)
; 2)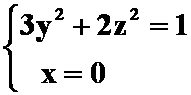 ;
;
3)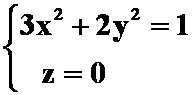
A.1) 2); B. 1) 3); C. 2) 3); D. 1) 2) 3);
解 ![]() 1)绕
1)绕![]() 轴旋转得
轴旋转得![]()
2)绕![]() 轴旋转得
轴旋转得![]()
![]() 选
选![]()
3.两平面![]() 的夹角为
( )。
的夹角为
( )。
A.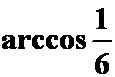 ; B.
; B. ![]() ; C.
; C. 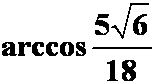 ; D.
; D. ![]() ;
;
解: 选C
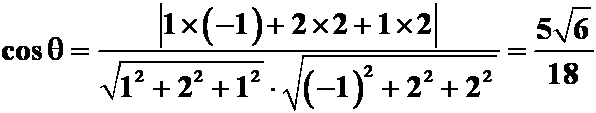
4.若两直线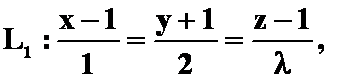
 相交,则
相交,则![]() ( )
( )
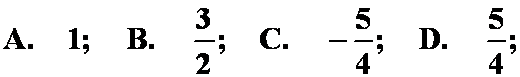
解: 设
得![]() 代入
代入![]()
得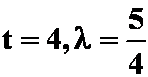 选D
选D
课后习题:
1求点D(3,1,3)到两向量
![]()
所在的平面的距离。(提示:![]() 投影到
投影到![]() 上)
上)
2.求点(-1,2,0)在平面![]() 上的投影。(提示:过此点作垂线)
上的投影。(提示:过此点作垂线)
3.求直线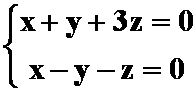 与平面
与平面![]() 的夹角。
的夹角。
4.证明两直线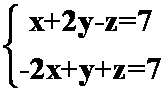 与
与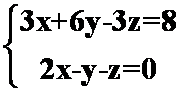 平行。
平行。
5.求点(-1,2,0)在平面![]() 上的投影。(提示:过此点作垂线)
上的投影。(提示:过此点作垂线)
6.求直线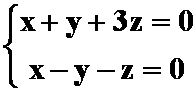 与平面
与平面![]() 的夹角。
的夹角。
7.证明两直线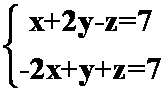 与
与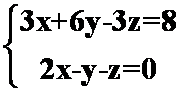 平行。
平行。