第八次习题课
内容:第六章 (物理应用不考)
重点:微元法,定积分在几何上的应用。
难点:微元法,极坐标求面积。
专题1 定积分元素法的要点
1.被求的量有一个“不变”状态下的乘积表达式(前提);
2.确定被积变量(如x)与被积的范围;
3.给出一个被积变量增量很小时的所求量的微元(如f(x)dx);
4.利用极限的思想,写出积分表达式。
例1:一个长为a的不均匀细棒,其线密度为![]() (x为到某一固定端点的距离)。求此细棒的质量。(答案:
(x为到某一固定端点的距离)。求此细棒的质量。(答案: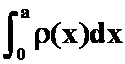 )
)
专题2 关于极坐标。
1.极坐标系:极点、极轴。极径,极角。
2.极坐标一般表示式:![]()
3.极坐标![]() 的范围:无限制时:
的范围:无限制时:![]() ,
,
(对有周期的函数往往取它一个周期)它唯一受r的限制:![]() 。
。
如:1)![]() 故
故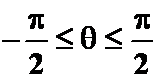 。
。
2)![]() ,故
,故![]() 。
。
4.常见的极坐标公式及其图形:
圆:![]() 或
或![]() 或
或![]()
(a为半径)
心形线:![]()
阿基米德螺线:![]()
5.极坐标与直角坐标的转换:
极坐标![]() 直角坐标:
直角坐标:
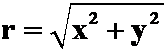
![]()
直角坐标![]() 极坐标:
极坐标:
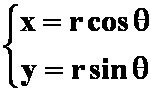
如:1)![]() 化成
化成![]()
2)![]() 化成
化成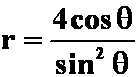
6.极坐标的对称问题:
若![]() ,图形关于极轴对称。
,图形关于极轴对称。
若![]() ,图形关于极点对称。
,图形关于极点对称。
如:心形线:![]() 关于极轴对称。
关于极轴对称。
双纽线:![]() 关于极轴与极点均对称。
关于极轴与极点均对称。
专题3:定积分的应用以及注意的问题
无论是几何应用或物理应用,其原理都是用元素法。
注意:以下所有的公式都是在标准的形式。对于具体问题,要学会变通!如果只会死套公式,学这一章就无意义了。
1.
求面积
注意:1)求面积关键要定出分界点以便分段以及上、下限对应的函数的大小。
定限方法:扫描定限:
直角坐标:横线竖扫,竖线横扫。
极坐标:射线旋转扫。
2)其次要考虑对x积分还是对y积分!
3)极坐标关键是要记住常见图形:圆、心形线,阿基米德螺线,的大致图形以及![]() 的范围。参数方程记住摆线、星形线即可。
的范围。参数方程记住摆线、星形线即可。
A.直角坐标系下: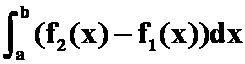
B.极坐标系下: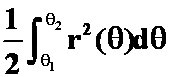
例2:(1)求由曲线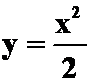 与曲线
与曲线![]() 所围成部分的面积。(答案:
所围成部分的面积。(答案:![]() )
)
提示: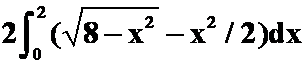
(2)(书280第4题)求抛物线![]() 及其在点(0,-3)和(3,0)处切线围成图形的面积。(答案见书后)
及其在点(0,-3)和(3,0)处切线围成图形的面积。(答案见书后)
提示:(0,-3) 切线:![]()
(3,0) 切线:![]()
切线交点:![]()
面积:
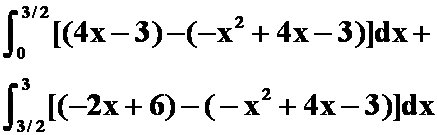
例3(1)(书280页8(1)题 )求曲线![]() 以及
以及![]() 所围成公共部分的面积。
所围成公共部分的面积。
(答案:书后有)
提示:注意画图。
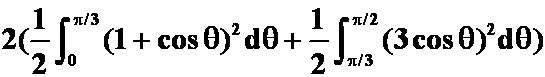
(2)圆![]() 被心形线
被心形线![]() 分成两部分,求这两部分的面积。
分成两部分,求这两部分的面积。
(答案: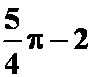 ,以及
,以及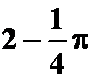 )
)
提示:![]() 为分界点。
为分界点。
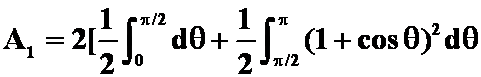
2.
求体积
注意:1)这里只能求旋转体的体积以及界面面积已知的物体体积(一般物体的体积下学期学)。
2)要注意是绕哪个轴旋转。
3)对于稍微复杂的图形的旋转,可以用“投影法”……
例4:求由圆![]() 绕x轴旋转所围成的环体的体积。(答案:
绕x轴旋转所围成的环体的体积。(答案:![]() )
)
提示:
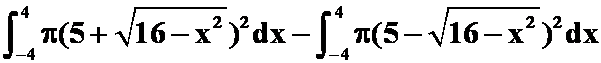
例5 分别求由曲线![]() 与直线x=a,x=
与直线x=a,x=
答案:(![]() ,
,![]() )
)
提示:x轴: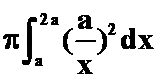
Y轴:(用微元法、投影法均可)
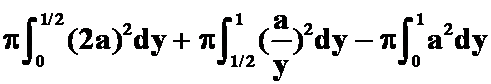
例6
设有一个椎体,底面为椭圆。底面椭
圆的长半轴为2,短半轴为1,高为3求其体积。(答案:![]() )
)
提示: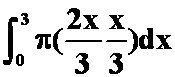
3.
求弧长
直角坐标下: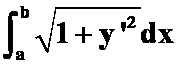
直角坐标参数方程下:
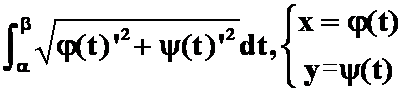
极坐标下:
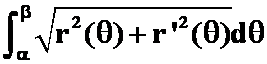
例7(书282页27题)在摆线![]() ,
,![]() 上,求分摆线第一拱成1:3的点的坐标。(答案:书后有答案 )
上,求分摆线第一拱成1:3的点的坐标。(答案:书后有答案 )
提示:设坐标对应参数为![]()
例8 计算曲线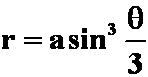 的全长
的全长![]() 。
。
(答案: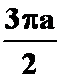 )
)
提示:注意![]() 的范围。
的范围。
补充习题:
选择题
1.
已知![]() 与
与![]() 所围成图形面积为
所围成图形面积为![]() ,则
,则![]() 的值
的值![]() 为 (
)
为 (
)
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
解 ![]() 与
与![]() 的交点:
的交点:![]()
则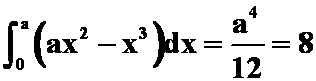 ,即得A。
,即得A。
2.由连续曲线![]() 。(这里
。(这里
![]() )及直线
)及直线![]()
所围成图形绕![]() 轴旋转一周所得的立体体积为
( )。
轴旋转一周所得的立体体积为
( )。
A.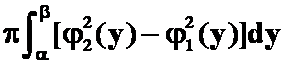 ;
;
B.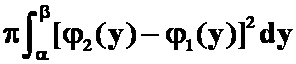 ;
;
C.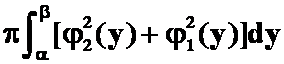 ;
;
D.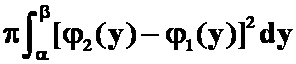 ;
;
解: 答案是A
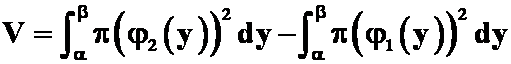
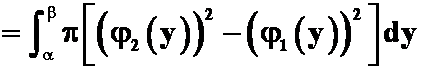
3.曲线![]() 与两坐标轴所围成图形面积为
( )。
与两坐标轴所围成图形面积为
( )。
A. ![]() ; B.
; B. ![]() ; C.
; C. ![]() ; D.
; D. ![]() ;
;
解 ![]() 与两坐标轴的交点为:
与两坐标轴的交点为:![]()
则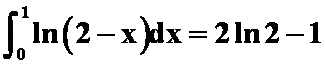 。故填A
。故填A
计算:
抛物线![]() 通过点
通过点![]() 两点,且
两点,且![]() 确定
确定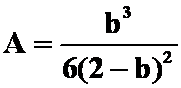 的值,使抛物线与
的值,使抛物线与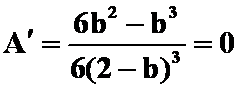 轴所围成图形面积为最小。
轴所围成图形面积为最小。
解![]() 抛物线过
抛物线过![]() 点
点 ![]() .
.
又过点![]() ,
,![]() ;
;
![]() ,
,![]() ,
,
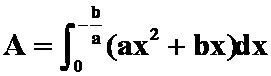
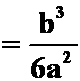 ;
;
将![]() 代入上式:
代入上式: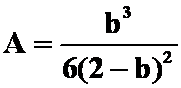 ,
,
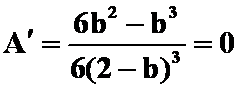 ,得
,得 ![]() (舍去),
(舍去),![]() ,
,
代入![]() 。
。![]()
课后练习:
1.求抛物线![]() 及其在点(
及其在点(![]() )处的法线所围成的图形的面积。
)处的法线所围成的图形的面积。
2.由y=![]() ,x=2,y=0围成的图形,分别绕x轴与y轴旋转,分别求旋转体体积。
,x=2,y=0围成的图形,分别绕x轴与y轴旋转,分别求旋转体体积。
3.计算阿基米德螺线![]() ,对应于
,对应于![]()
到![]() 的一段弧对应极轴所围成的面积。
的一段弧对应极轴所围成的面积。
4. 求曲线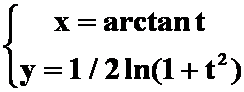 自t=0至t=1的一段弧。
自t=0至t=1的一段弧。