第七次习题课
内容:第五章
重点:求定积分,变上限积分。
难点:变上限积分的求导、反常积分。
专题:定积分的计算方法
1.
利用不定积分求;
2.利用被积函数的性质求。
例1 求下列定积分
(1)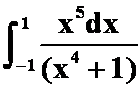 答案:0
答案:0
答案:0; 提示:奇函数对称区间。
注意:对于反常积分失效!如:
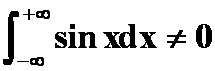 (不存在!)
(不存在!)
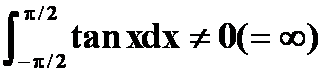
(即使答案正确也不能用奇(偶)函数!)
(2)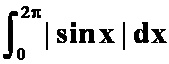 答案:4
答案:4
(3)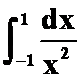 答案:发散
答案:发散
(注意:不是一般定积分!有瑕点。(这在不定积分中不需要考虑,因为无需定限。)
(4)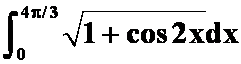 答案:
答案: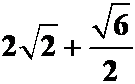
注意:去根号时要打绝对值。
例2:求下列定积分
(1)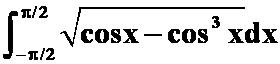 (答案:4/3)
(答案:4/3)
(2)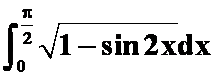 (答案:
(答案: ![]() )
)
(3)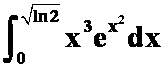 (答案:
(答案:![]() )
)
(4)求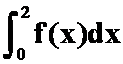 ,其中
,其中
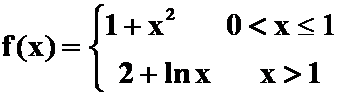
(答案:![]() )
)
(5)设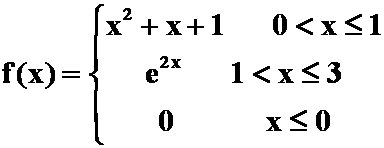 ,求函数
,求函数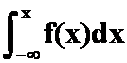 在
在![]() 的表达式。
的表达式。
答案:

专题:定积分的性质的作用以及变上限积分
1.利用定积分的性质解题
例3:估计积分值
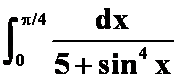
(答案:在[![]() ,
,![]() ]之间)
]之间)
2.证明题
例4 若在[a,b]上,f(x)连续,且![]() ,
,
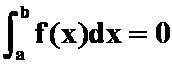 ,证明在[a,b]上,f(x)
,证明在[a,b]上,f(x)![]() 0
0
提示:反证法。连续函数的性质。
例5 证明: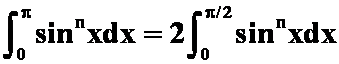 。
。
提示:积分区间对半分,然后换元。
3.变上限积分的求导
例6:(1)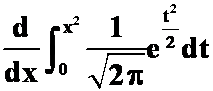
(答案: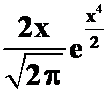 )
)
注:两类不定积分
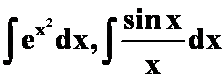
直接积分不可能积出,下题同。
(2)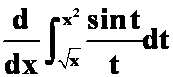
(答案: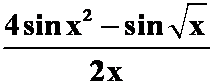 )
)
(3)求极限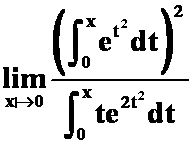
(答案:2)
2.
数学中动态量,变量,常量问题初探:
1)
概念:
常量:任何时候都不改变的量。
变量:研究函数等问题时,一个量可以取不同的值。这样,往往用一个字母来代替。这叫变量。如![]() 中的x与y。
中的x与y。
动态量:研究极限问题时,往往要求变量趋向(朝某方向运动。)于某值,这样的变量是“动态量”。如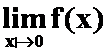 中的x。
中的x。
2)
三者关系:
动态量是变量、变量运动时是动态量;
变量取定某值时为常量;
三者之间有时可以相互转化。
3)
数学中处理变量的原则:逐一处理。
如:(1) 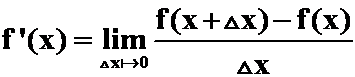 在求极限过程中
在求极限过程中![]() 是动态量(也是变量),x暂时作“常量”。
是动态量(也是变量),x暂时作“常量”。
(2) 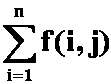 在连加中i为变量,j暂时作“常量”。
在连加中i为变量,j暂时作“常量”。
(3)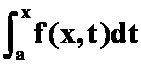 在积分过程中t为变量。x暂时作为“常量”.
在积分过程中t为变量。x暂时作为“常量”.
4)变量的分类:
离散型:变量活动的范围是有限个或无限可列个数值,这样的变量是离散型变量。
连续型:变量活动的范围是无限不可列个数值,如区间[a,b],量是连续型变量。
离散型与连续型变量有时是特殊性与一般性的关系。做题时可以互相利用。
5)量的替换的原则:
等量替换 。。。,动态量替换。。。,常量与变量互换,。。。常量与动态量的互换。。。
例:(1)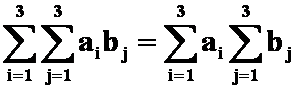
(2)
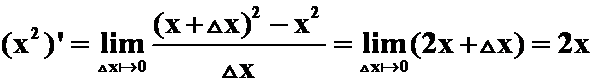
(3)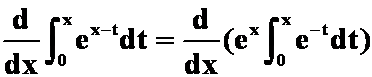
专题:反常积分的问题
反常积分的关键在于要学会判别是否反常积分以及反常积分的种类。
例7:求下列定积分
(1)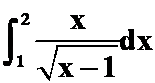 (答案:8/3)
(答案:8/3)
(2) 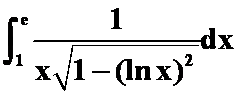 (答案:
(答案:![]() )
)
注:换元时暂不考虑是否有无穷间断点。有时换元后变成了正常积分!
例8:求下列定积分
(1)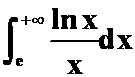 (答案:发散)
(答案:发散)
(2)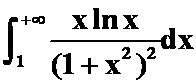 (答案:
(答案: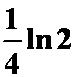 )
)
(3)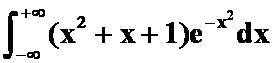 (答案:
(答案: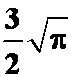 )
)
补充习题:
选择题
1.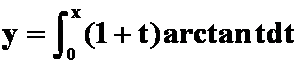 的极小值是( )
的极小值是( )
![]()
![]()
![]()
![]()
解:![]()
![]()
驻点为 ![]()
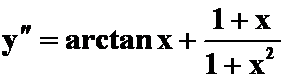
当![]()
![]() ,
,![]()
![]()
![]() 时,
时,![]() 取极小值
取极小值![]() 选B。
选B。
2. 设![]() 在
在![]() 上连续,则
上连续,则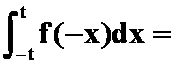 ( )。
( )。
![]() ;
;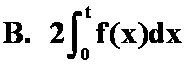 ;
;
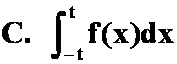
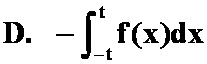 ;
;
解 令![]() ,则
,则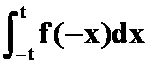
=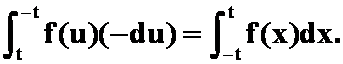 故
故![]()
3.设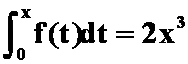 ,则
,则
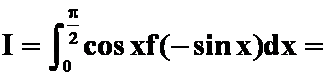 ( )。
( )。
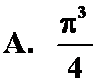 ;
; 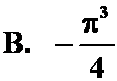 ;
; ![]() ;
; ![]() ;
;
解 I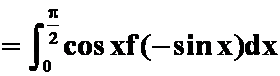
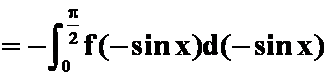
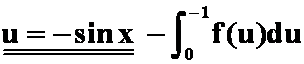
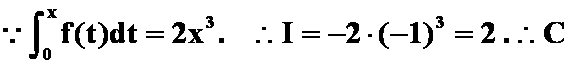
7.证明:利用定积分的性质证明:
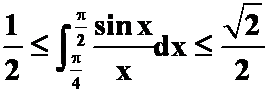
证明: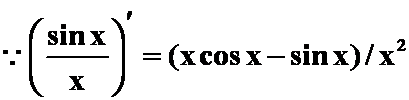
令y=![]() ,
,![]()
又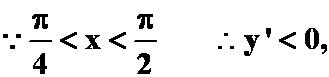
而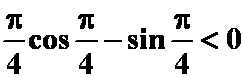 ,故
,故![]() ,所以:
,所以:
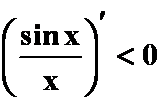
即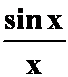 在
在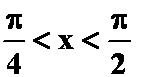 内单调递减
内单调递减
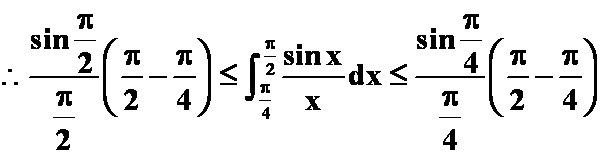
也即 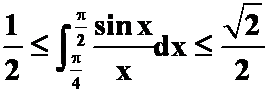
课后作业:
1.求下列定积分(注意判断反常积分)
(1)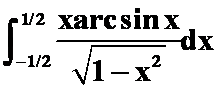
(2)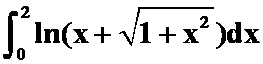
(3)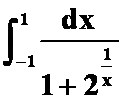 (非反常积分,积分区间对半然后换元)
(非反常积分,积分区间对半然后换元)
2.求极限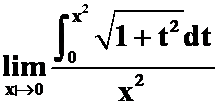
3.证明:已知f(x)连续,证明:
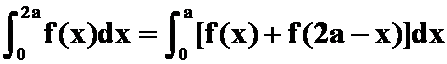
提示:积分限分一半,然后对后面一半令x=