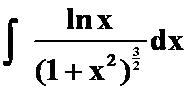第六次习题课
内容:第四章
重点:不定积分的计算。
难点:凑微分法计算不定积分。
专题1 不定积分计算的方法与技巧
1.
基本公式法(较少见)
例1 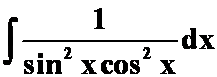
(答案:![]() )
)
2.
凑微分法—第一类换元法(优先考虑)
本质:原函数是复合函数。
此类方法非常灵活。但是,也还是能找到一些普遍适用的规律,总结如下:
甲求导后得乙,
无理变成有理,
三指凑成一类,
幂次化出整倍。
此口诀也适用于第二类换元法与分部积分法。待到上课解释。
例2 求下列不定积分
(1)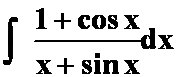 “甲求导后得乙”
“甲求导后得乙”
答案:![]()
(2)
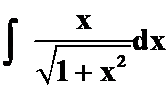 “无理变成有理”
“无理变成有理”
答案:![]() +C
+C
(3)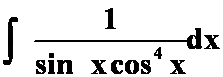 “三角凑成一类”
“三角凑成一类”
答案:
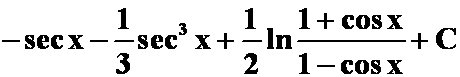
(4)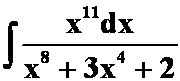 “幂次化出整倍”
“幂次化出整倍”
答案:
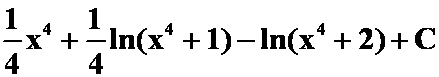
(5)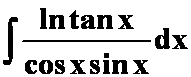 “三角凑成一类”
“三角凑成一类”
解:原式=
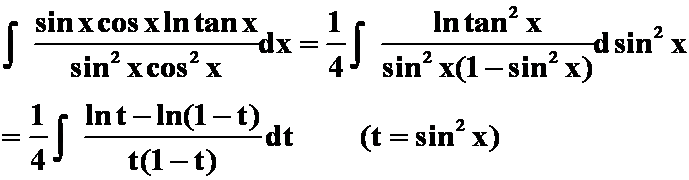 (以下计算略)
(以下计算略)
答案:
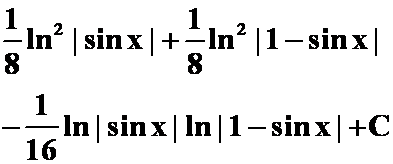
(6)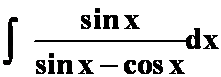
答案: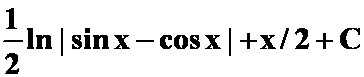
(7)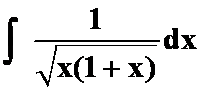
注:直接令t=![]() 不好。先凑微分再主动(第二类)换元。
不好。先凑微分再主动(第二类)换元。
答案:![]()
(8) 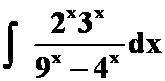 (指数也可以化成一类)
(指数也可以化成一类)
答案: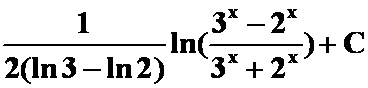
3.第二类换元法
与第一类换元法不同,其原函数并非复合函数。是因为为了去根号等原因人为将自变量作为中间变量。
先对凑微分来说,第二类换元法较有规律,一般的原则是:
1.![]() 型,令x=asint
型,令x=asint
2. ![]() 型 令x=atant
型 令x=atant
3 ![]() 型 令x=asect
型 令x=asect
4. 倒代换(少见):针对分母幂次较高的情形,可将分母的幂化为分子的幂。
5.最小次幂代换:当出现不同次的根号时,直接用凑微分不易求时考虑用它。
6.万能公式代换:能将三角被积函数化有理函数。(缺点是较繁琐,其它方法不灵时用)
……
注意:有的函数含有上面的形式的项,但是并不需要用第二类换元法。如:
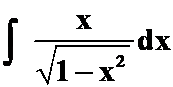
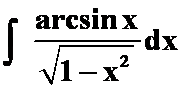
例3 求下列不定积分:
(1)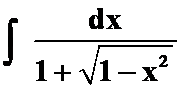 (注意最后的转化)
(注意最后的转化)
(答案: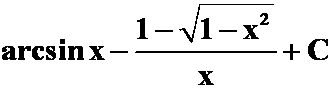 )
)
(2)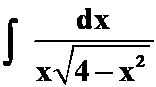
(提示:令![]() 或令x=2sint,或x=1/t,答案:1/2
或令x=2sint,或x=1/t,答案:1/2 )
)
(3)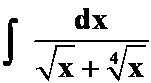
(提示:最小幂代换,令![]() )
)
(4)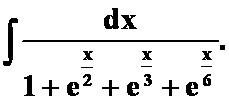
(提示:最小幂代换,令![]() )
)
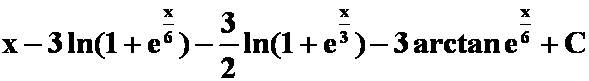
(5)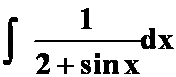 (提示:万能公式置换)
(提示:万能公式置换)
答案: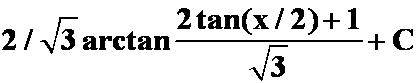
(6)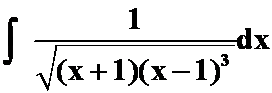
提示:令 ,最后可以化幂函数。
,最后可以化幂函数。
4.分部积分法
此方法被积函数往往是有两类函数相乘。其根据是函数乘法的导数公式。
此方法归纳起来, 总结成一句话,就是“反对幂指三,前导后积莫乱来!”(前半句话每一个字表示一类初等函数。)
分部积分的目的:1)对幂函数降幂最终消去幂函数;2)对反三角函数(对数函数)求导变成其它易积函数;3)循环求积分(往往针对三角函数;4)求递推式(少用)。
例4:求下列不定积分
(1)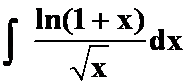 (“对”与“幂”)
(“对”与“幂”)
答案:
![]()
(2)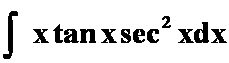 (“幂”与“三”)
(“幂”与“三”)
答案:![]()
(3)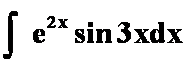 (“指”与“三”)
(“指”与“三”)
(4)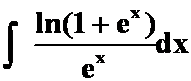 (“对”与“指”)
(“对”与“指”)
答案:![]()
(5)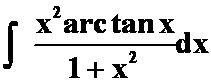 (“幂”与“反”)
(“幂”与“反”)
答案:
![]()
(6)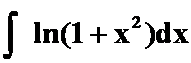 (“对”:可看成“幂”与“对”)
(“对”:可看成“幂”与“对”)
(7)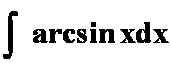 (“反”:可看成幂与反)
(“反”:可看成幂与反)
(8)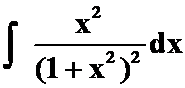 (分部,降幂)
(分部,降幂)
答案: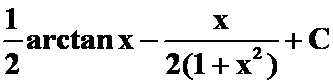
5.有理函数的积分法(最后用此法)
有理函数的积分一般方法没有什么技巧。在凑微分不灵时用。即使裂项,除了不得已之外,有时也可以避免待定系数。
例5:求下列积分
(1)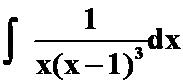
提示:
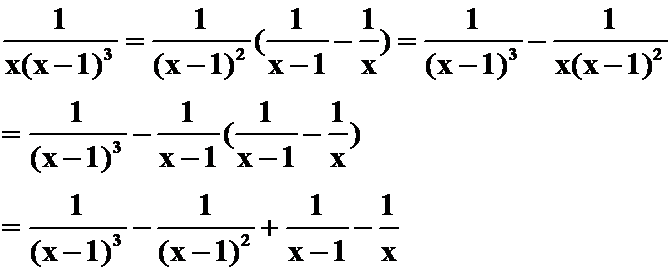
(2)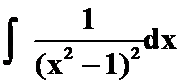
提示:

(3)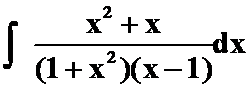
提示:
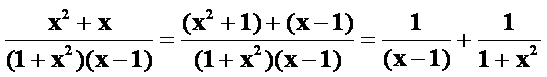
(4)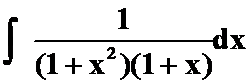
提示:此题看来没法凑微分,也没什么好技巧。只好用常规方法。一般若待定系数3个以下就直接用比较方便。
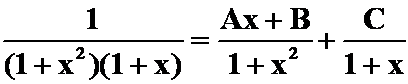
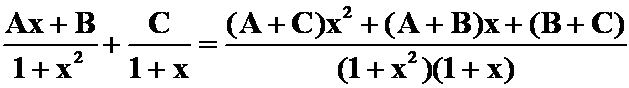
补充题
选择题:
1. 若函数![]() 与
与![]() 满足
满足![]() ,则必有
( )
,则必有
( )
A.![]()
B.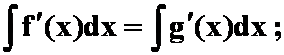
C.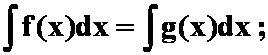
D.![]() 。
。
选B
2. 对积分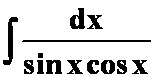 而言,下列答案中不正确的是 ( )。
而言,下列答案中不正确的是 ( )。
A.![]()
B. ![]()
C.![]()
D. ![]() 。
。
解 选(D)。
3.对积分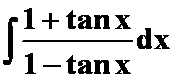 而言,下列答案中不正确的是( )。
而言,下列答案中不正确的是( )。
A.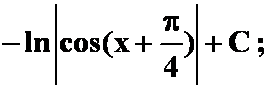
B.![]()
C.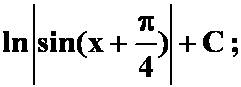
D.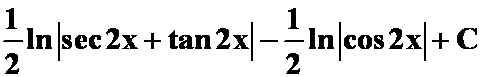 。
。
解 选(C)。
课后习题:
计算下列不定积分
(1)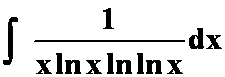 (2)
(2)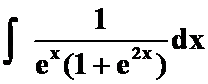
(3)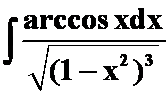
(提示:先求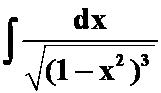 )
)
(4)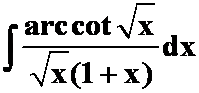 (5)
(5)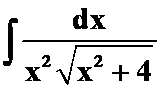
(6)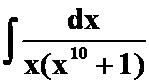 (7)
(7)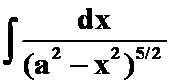
(8)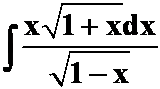 (提示:先分子有理化)
(提示:先分子有理化)
(9)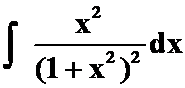 (提示:分部积分)
(提示:分部积分)
(10)
(提示:先凑![]() 再第二类换元)
再第二类换元)
(11)