第五次习题课
内容: 第三章第四节至第七节
重点: 函数各类性状的描述;函数作图。
难点: 曲率;利用函数的性状证明题目。
专题 函数的性状的总结
1.
单调性以及极、最值点;
注意:极值与最值的关系;对于可导函数,驻点是极值点的必要非充分条件。
2.
凹凸性以及拐点;
注意:若函数有二阶导,![]() 是函数凹(凸)的充分条件。不是必要条件!
是函数凹(凸)的充分条件。不是必要条件!
![]() 是拐点的必要条件。
是拐点的必要条件。
3.
渐近线;
渐近线取决于无穷远点的极限。
铅直渐进线x=a: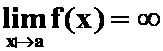
水平渐近线y=b:
![]()
4.
奇偶性:若是奇函数(或偶函数)就只需要考虑半边。
5.
周期性:若是周期函数就只需要考虑一个周期。
说明:函数的奇偶性与周期性与函数的导数没有关系。但是在描绘函数图形时不可不考虑它们。
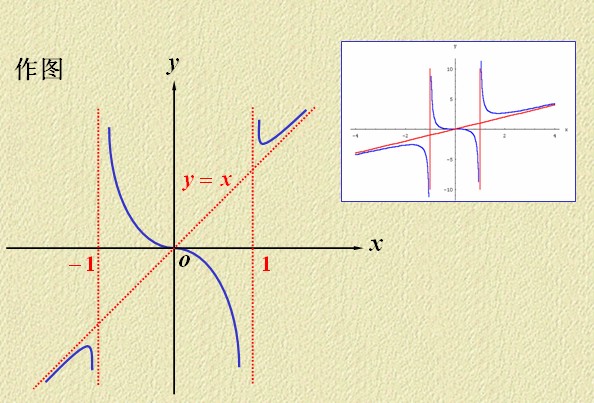
例1:求函数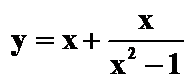 的图形
的图形
解:定义域:![]() 奇函数;
奇函数;
![]()
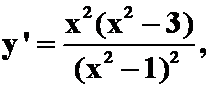 驻点:
驻点: ![]()
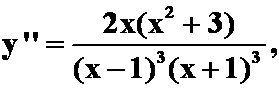 拐点:x=0
拐点:x=0
无水平渐近线,铅直渐进线:x=1与x=-1
斜渐近线:y=x

专题:函数的极值与最值
单纯函数的极值与最值的求法比较简单,按书中步骤即可。具体问题的最值往往只有一个驻点。这个驻点一般不必判断就是最值点。
例2 某地区防空洞的截面拟建成矩形加半圆。截面的面积为5![]() 。问底宽x为多少时才能使界面的周长最小,从而使建造时的材料最省。
。问底宽x为多少时才能使界面的周长最小,从而使建造时的材料最省。
提示:面积![]()
周长: 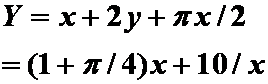
答案:底宽:
例3 求函数y=![]() 在[-5,1]的极值与最值。
在[-5,1]的极值与最值。
答案:最大值:![]() 最小:
最小:![]()
极大:![]() 无极小值。
无极小值。
专题:利用函数的性状证明题目:
1. 利用函数的单调性证明不等式
特点:不等式的某一边是单调函数(用求导判)。
例4:证明:当![]() 时,
时,
![]() 。
。
证明: 令
![]()
当![]() 时,
时,![]() 连续,
连续,
且![]()
则![]() 在
在![]() 时单调增加,即
时单调增加,即![]() 时
时
![]()
![]()
2.利用函数的单调性证明方程的根的个数
依据:方程的根对应函数的零点。
例5.证明方程![]() 有且仅有一个实根。
有且仅有一个实根。
提示:令![]() 。利用单调性证明至多只有一个实根。在[0,2]上利用介值定理证明存在一个根。
。利用单调性证明至多只有一个实根。在[0,2]上利用介值定理证明存在一个根。
有了导数与单调性的关系后,一般方程的根的个数以及范围均可以确定下来!
3.利用函数的凹凸性证明不等式
特点:1)有相同结构的和;
2)有中点值;3)单边不等式。(注意与中值定理的条件比较)
例6: 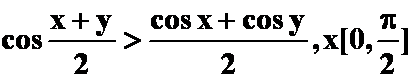
提示:令y=cosx
4.总结:到现在为止,证明不等式的常用方法有以下:
1)
利用中值定理;(运用原则见上次习题课)
2)
利用泰勒公式;(不作要求)
3)
利用函数的单调性与极(最)值;
4)
利用函数的凹凸性.
例7 现在给出几个不等式的证明题目,请同学们判断它们各用什么方法证明并证明之。
(1)
证明:当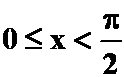 时,tanx-x
时,tanx-x![]() 0
0
(2)
证明:![]()
![]()
(3)证明:
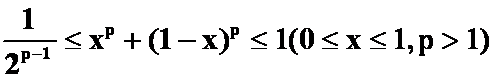
(4)对于![]() ,证明
,证明
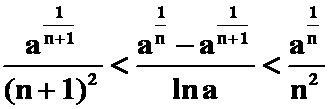
提示:(1)用单调性;![]() [0,
[0,![]()
(2)用凹凸性;![]() 在[a,b]
在[a,b]
(3)用函数最值;![]()
(4)用中值定理。![]() 在
在
补充练习:
选择题:
1对数曲线![]() 上哪点处的曲率半径最小
( )
上哪点处的曲率半径最小
( )
A.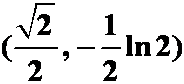 ;B.
;B.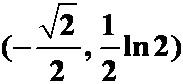 ;C.
;C.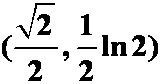 ; D.
; D.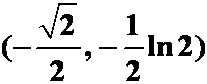 。
。
解 选(A)。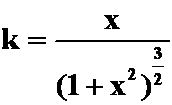 ,令
,令![]() 得
得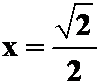 。
。
2.设偶函数![]() 具有连续的二阶导数,且
具有连续的二阶导数,且![]() 则
则![]() ( )。
( )。
A.不是![]() 的驻点;
的驻点;
B.一定是![]() 的极值点;
的极值点;
C.一定不是![]() 的极值点;
的极值点;
D.是否为![]() 极值点,还不能确定。
极值点,还不能确定。
解:选(B)![]() 是偶函数,
是偶函数,![]()
得![]() 。
。
3.曲线![]() 的曲率的最大值为( )。
的曲率的最大值为( )。
A.![]() ; B.
; B.![]() ; C.
; C.![]() ; D.
; D.![]() 。
。
解 选(B)。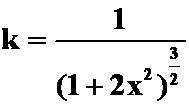 ,当
,当![]() 时,
时,![]() 。
。
4.对数曲线![]() 上哪点处的曲率半径最小
( )。
上哪点处的曲率半径最小
( )。
A.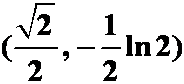 ;B.
;B.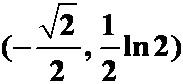 ;C.
;C.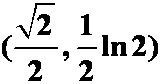 ; D.
; D.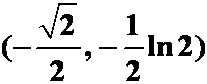 。
。
解 选(A)。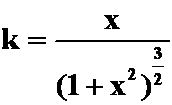 ,令
,令![]() 得
得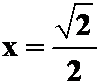 。
。
课后习题:
1.
画出函数 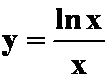 的图形。
的图形。
2.
证明:![]() 时,
时,![]()
3.一个半径为![]() 的球内有一个内接正圆锥体,问圆锥体的高和底半径成何比例时,圆锥体的体积最大?
的球内有一个内接正圆锥体,问圆锥体的高和底半径成何比例时,圆锥体的体积最大?
4.设![]() ,利用最值证明不等
,利用最值证明不等
式:![]() 。
。
提示:令![]() ,
,