第四次习题课
内容: 第三章第一节至第三节
重点: 拉格朗日中值定理;用洛必达法则求极限;函数的泰勒展开与近似计算。
难点: 柯西中值定理。
专题1 微分中值定理的应用
中值定理有四个,其中罗尔定理可以看成是拉格朗日中值定理的特殊情形。拉格朗日中值定理是柯西中值定理的特殊情形。柯西中值定理用得比较少。泰勒中值定理是拉格朗日中值定理的另一种推广.
1. 证明不等式
适合用中值定理的不等式一般具备下列几个条件:1)具有相同结构的差值;2)有导数的影子;3)双边不等式。
例1设![]() 证明:
证明:
![]()
提示:令![]() ,利用拉格朗日中值定理。
,利用拉格朗日中值定理。
例2 证明: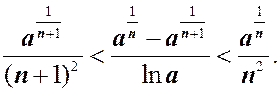
提示:令![]() ,用拉格朗日中值定理。
,用拉格朗日中值定理。
(对a讨论)
2.证明方程根的存在性
例3 若方程![]()
有一个正根![]() ,证明:方程
,证明:方程
![]()
必有一个小于![]() 的正根.
的正根.
提示:用罗尔定理。区间[0,![]() ]。
]。
例4 设函数
![]() ,
,
则方程![]() 有( ).
有( ).
(A)一个实根 (B)两个实根
(C)三个实根 (D)无实根
解析:利用罗尔定理
答案:(C).
3.证明函数导数的状况
例5 设![]() 在
在![]() 上连续,在
上连续,在![]() 内可导,证明(1)在
内可导,证明(1)在![]() 内至少存在一点
内至少存在一点![]() ,使
,使
![]() .
.
(2)若![]() ,则对于任意
,则对于任意![]() ,存在
,存在![]() ,使
,使![]() ,
,
例6 设f(x)在[0,1]上连续,在(0,1)内可导。f(1)=1。试证至少存在一点![]() ,使得
,使得 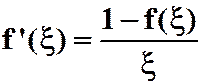 .
.
提示:用拉格朗日中值定理。
例
证明:F(x)=![]() 在(0,1)内存在c,使得
在(0,1)内存在c,使得![]()
例8 设![]() 在
在![]() 上连续,在
上连续,在![]() 内可导
内可导![]() ,证明:存在
,证明:存在![]() ,
,![]() ,使得
,使得 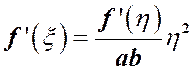 .
.
提示:待证式变形为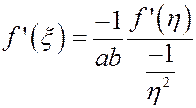 ,提示通过拉格朗日中值定理确定
,提示通过拉格朗日中值定理确定![]() ,再对
,再对![]() 和
和![]() 在
在![]() 上利用柯西定理即证.
上利用柯西定理即证.
专题2 洛必达法则求极限以及注意的问题
1. 每一次求导前均注意是否未定型;
2. 求导后若极限不存在不要贸然下结论;
3. 常常结合其它方法使用,不要一看到未定型就用它。
例5:求下列极限
(1)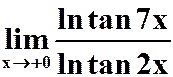 (答案:1 )
(答案:1 )
(2)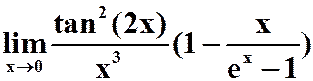 。
。
(答案:2)
(3)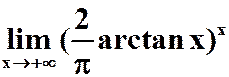
提示:用换底公式 答案: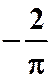
专题3 函数的泰勒展开
1. 泰勒公式展开方法:
(1) 直接法
求高阶导比较方便易找规律时用此法。注意有两种形式的余项:拉格朗日型与佩亚诺型。按照题目要求做。前者常用来估计误差,后者简便。它们其实是等价的!
例6 分别求y=![]() 在x=0 与x=1点的泰勒展开式。
在x=0 与x=1点的泰勒展开式。
答案:
X=0: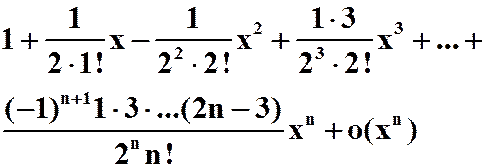
X=1:
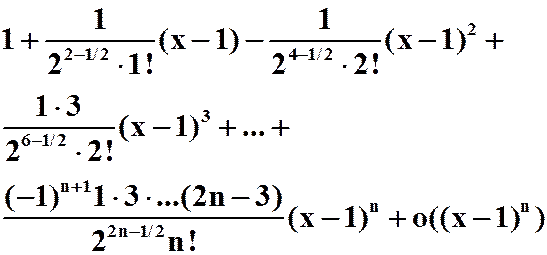
例7写出按![]() 的乘幂展开多项式
的乘幂展开多项式![]() 的表达式。
的表达式。
答案:
![]()
![]()
(2) 间接法:
此法相对灵活,就是不直接按部就班求导,而是分部分求导或通过变量代换利用原来的已知公式展开。
例8 求![]() 的带拉格朗日型余项的麦克劳林展开式。
的带拉格朗日型余项的麦克劳林展开式。
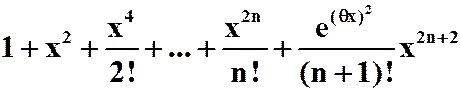
例9 求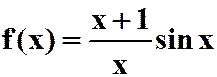 的带佩亚诺型余项的马克罗林展开式。
的带佩亚诺型余项的马克罗林展开式。
答案:
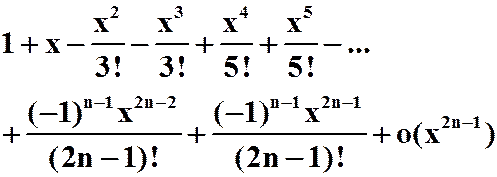
2. 函数的泰勒展开的用途
(1) 利用多项式函数近似代替一般函数。
说明:泰勒公式与微分都是求近似。
联系:微分公式可以看成一阶泰勒公式。
泰勒公式优点:精确可控;缺点:复杂。
微分公式优点:简单;缺点:不算很精确,不可控。
例10 用二阶泰勒公式求![]() 的近似值,并估计误差。然后用微分求一遍它的近似值,以此验证两种方法的优劣。
的近似值,并估计误差。然后用微分求一遍它的近似值,以此验证两种方法的优劣。
答案:泰勒:
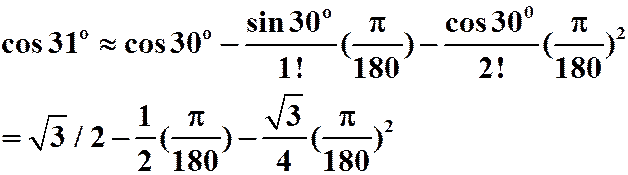 =0.8571
=0.8571
误差小于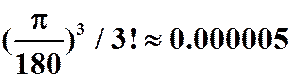
微分: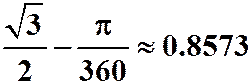
(2)利用泰勒公式求极限(少用)
例11 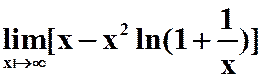
(提示:将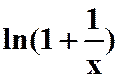 展开,答案:1/2)
展开,答案:1/2)
(3)证明不等式
注:此种方法较难。作为本科生不作太多要求。
例12:证明:![]() 时
时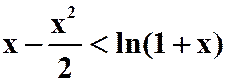
提示:将![]() 作泰勒展开。
作泰勒展开。
(4)证明函数的导数等性状
说明:我们发现,泰勒公式与微分中值定理有相似的功用。这是因为泰勒公式中的末项用到了中值定理。
例13 证明f(x)是n次多项式的充要条件是![]() 。
。
提示:关键是充分性的证明。
补充习题:
一.选择题
1.在区间![]() 上满足罗尔定理条件的函数是
( )
上满足罗尔定理条件的函数是
( )
A.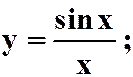 B.
B.![]()
C.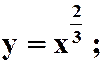 D.
D.![]() 。
。
2.![]() 在
在![]() 可导且
可导且![]() ,则( )
,则( )
(A) 至少存在一点![]() ,使
,使![]() ;
;
(B) 一定不存在点![]() ,使
,使![]() ;
;
(C) 恰存在一点![]() ,使
,使![]() ;
;
(D)对任意的![]() ,不一定能使
,不一定能使![]() 。
。
3.下列各式应用罗必达法则正确的是( )。
A.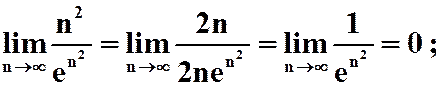
B.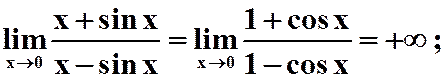
C.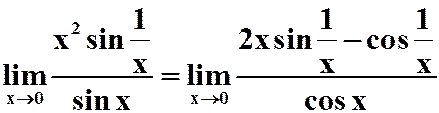 不存在;
不存在;
D. 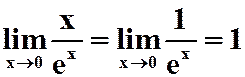 。
。
解
选(B)。A,D:不能用洛必达法则;C: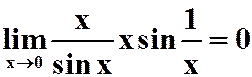 。
。
课后习题:
1.若f(x)在[a,b]有n阶导,且
![]()
证明在(a,b)内至少存在一点![]() 使得
使得![]() 。
。
2利用罗比达法则求极限
(1)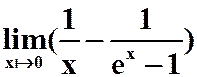 (2)
(2)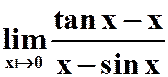
3. 利用泰勒公式求极限:
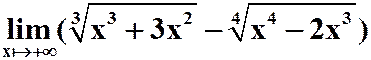
4.将函数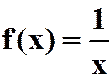 按(x+2)的幂展开的带有拉格郎日余项的泰勒公式。
按(x+2)的幂展开的带有拉格郎日余项的泰勒公式。