总复习2
考试题型分析:
填空与选择:填空题一般有。具体可能如求极限;简单的偏导;方向导数与梯度;不复杂的函数的极值;一般级数的敛散性判别;较规范的微分方程的特解等。
计算:大部分。求导中复合函数的偏导常见,方程组确定的隐函数基本没有。重积分中三重积分以球面柱面积分为多。曲线积分常常优先考虑格林公式;曲面积分常常优先考虑高斯公式。级数展开、级数判断是重点,分数较多也好拿。
证明:较少,少数集中在重积分与级数
方面。
应用:极少。限制在比较浅显的几何应用。比如第一章中的偏导的几何应用。
注意的问题:
求导方面:
1.多元函数隐函数的求导对多个变量的关系分析不清。
2.复合函数的求导当一个变量既作中间变量又作自变量时出现混乱。
例:对![]() 求x的偏导。
求x的偏导。
错解: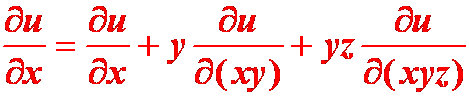
正解: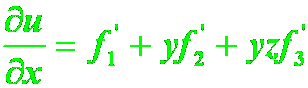
3.对“形式”的偏导认识不清楚。
错例:求隐函数![]() 的导数:
的导数:  正解:
正解: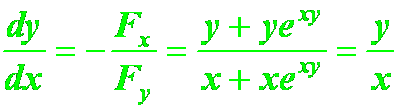
积分方面:
4.二重积分化累次积分时不注意积分顺序而增加工作量或出错。
错例:
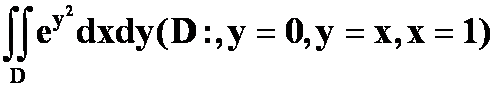
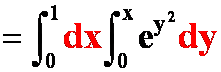 (积不出)
(积不出)
正解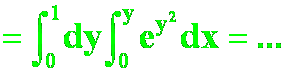
5.二重积分定限混乱:
1)定限顺序混乱,如后积的出现函数(应该是常数)。
错例: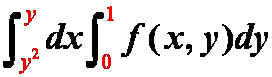
2)极坐标转换忘记加“r”。
6.极坐标求二重积分中扫描方式等同于直角坐标。
错例:D:x轴,x=1,y=x围成,
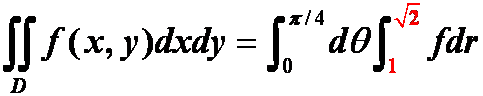
正解: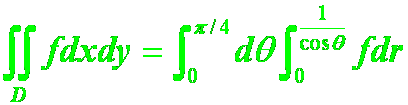
7. 三重积分:
1)柱面坐标与球面坐标的扫描方式混淆。
错例:![]() 围成的闭区域。错解:
围成的闭区域。错解:
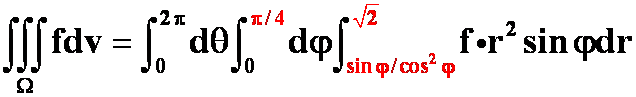 正解:
正解: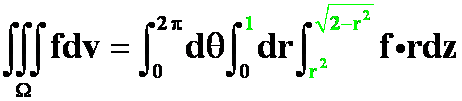
2)三重积分中“先一后二”与“先二后一”
用不好。定限时张冠李戴。
3)被积函数与积分限函数混淆。如求曲面面积时不能将被求曲面表达式作为被积函数!
错例:求曲面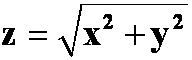 被
被
![]()
截得的部分的面积。
错解:
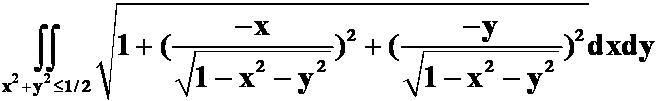 正解:
正解:
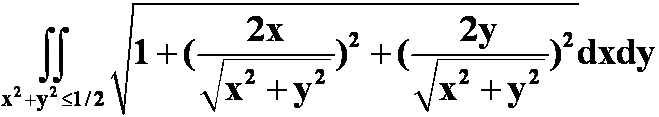
4)柱面坐标(或球面坐标)忘记加r(或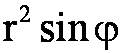 )或者加反。
)或者加反。
8.曲线积分。
1)用格林公式没有判断条件(没有注意到瑕点(即不可微的点))。
错例: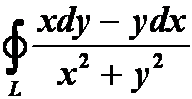
L:x轴上方![]() 中从x=1到x=-1的一段弧。
中从x=1到x=-1的一段弧。
错解:据格林公式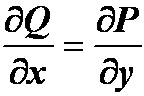 ,原式=0
,原式=0
2)第一类曲线积分化参数的定积分注意上限大于下限。
9.曲面积分
1)用高斯公式时,曲面的方向问题模糊。
2)对投影有重叠的曲面不知道如何处理。(投影时尽量避免重叠)
级数部分
10.数项级数的审敛时将必要条件![]() 当充分条件。
当充分条件。
11用放缩法方向用反
错例:因为 ,而
,而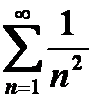 收敛,所以
收敛,所以 收敛。
收敛。
12.一般项级数的审敛当做正项级数审敛。
13.数项级数的比较审敛法的极限形式与比值审敛法混淆。
错例:因为
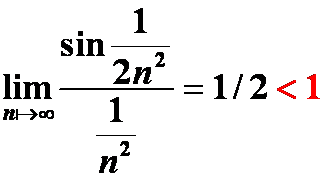
所以级数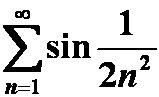 收敛。
收敛。
14.求和函数没有注意首项。
微分方程部分
15.对线性微分方程中的“线性”理解不清导致判断错误。
16.二阶常系数线性微分方程中,特解的指数函数中的指数中x的系数与对应通解中特征方程的系数混淆。
17.遇到二阶非齐次常系数方程时f(x)有三角函数时分辨不清情况。
错例:![]()
特征方程的根r=1,-3;从![]()
可见![]() ,是单根…
,是单根…
正解:从![]() 得
得![]() ,
,![]() ,非根。。。
,非根。。。
18 用曲线积分求全微分方程时折线积分代值混乱。
错例:L为折线:(0,0)->(x,0)->(x,y)
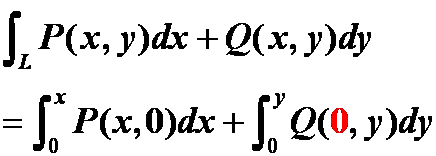
19 凑微分时遇到两个变量时处理混乱。
错例:1)ydx=dxy
2)
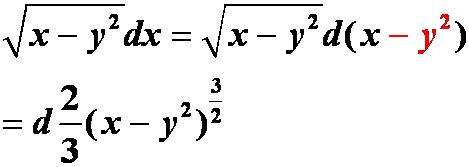
再问:
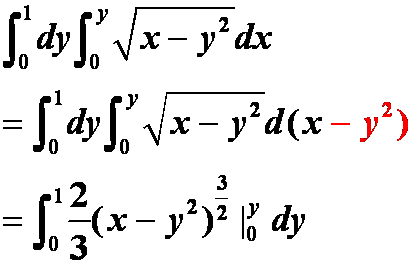
可不可行?为什么?
答:可行!对定积分中后面的![]() 不能理解成
不能理解成![]() 的微分。因为前面有dy,后面的应该将y当“常量”!
的微分。因为前面有dy,后面的应该将y当“常量”!