总复习1
典型例题精选
一、计算
1、极限与连续。
*例1 求极限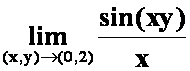 (05-06)A
(05-06)A
提示:利用重要极限。
答案:2。
例2判断极限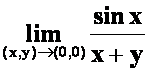 是否存在。
是否存在。
提示:不存在。取直线族![]() 。
。
2、多元函数求偏导;极值与最值。
*例3 设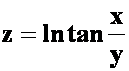 ,(1)求
,(1)求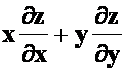 (2)设
(2)设![]() ,求全微分
,求全微分![]() (03-04)
(03-04)
答案:(1)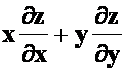 =0
=0
(2)
![]()
**例4 ![]() ,其中
,其中![]() 有二阶连续偏导数,求
有二阶连续偏导数,求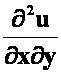 。(02-03)
。(02-03)
答案:
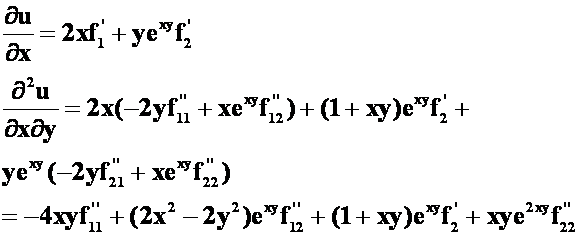
**例5 在第一卦限做椭球面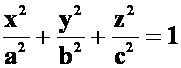 的切平面,使得该切平面与三坐标面所围成的四面体的体积最小,求切点的坐标。(07
的切平面,使得该切平面与三坐标面所围成的四面体的体积最小,求切点的坐标。(07
提示:切平面的方程:
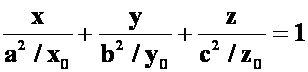
四面体体积: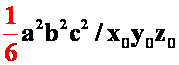 ,拉格朗日乘数法:
,拉格朗日乘数法:
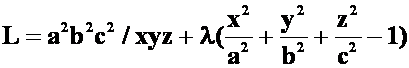
提示:运算讲究技巧。(利用对称)
答案:切点坐标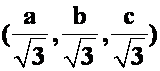
**例6 ![]() ,求
,求![]()
答案: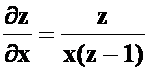 ;
;
*例7 若函数![]() 在点
在点![]() 处取得极小值,求a。
处取得极小值,求a。
答案:a=-5.
*例8求函数![]() 在点
在点![]() 处的梯度和沿该梯度方向的方向导数。(04-05)
处的梯度和沿该梯度方向的方向导数。(04-05)
答案:梯度:![]() ;梯度方向的方向导数:
;梯度方向的方向导数:![]() 。
。
例9求曲线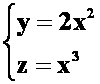 在点(1,2,1)处的切线方程与法平面方程。(08-09)
在点(1,2,1)处的切线方程与法平面方程。(08-09)
答案:切线: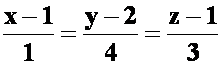
法平面:![]()
2、二重积分与三重积分。
*例10 计算二重积分
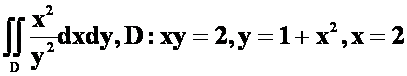
围成的区域。
答案: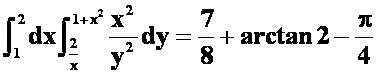
*例11求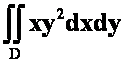 ,其中D是闭圆域
,其中D是闭圆域![]() (05-06)
(05-06)
提示:利用对称性。
答案:0。
*例12交换积分次序并计算: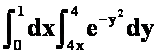 (04-05)
(04-05)
答案: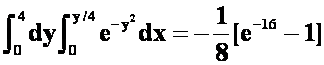
**例13 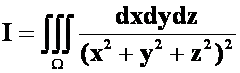 ,
,![]() 由
由![]() 确定。(05-06)
确定。(05-06)
提示:利用球面坐标(此题柱面不好算)。
答案: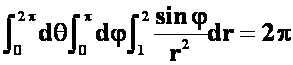
**例14求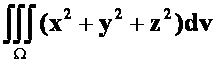 ,其中
,其中![]() 为上半球体
为上半球体![]() (08-09)
(08-09)
提示:用球面坐标。
答案: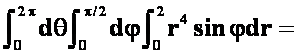
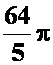
注意:不能将被积函数代4。
**例15 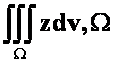 由锥面
由锥面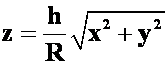 与平面
与平面![]() 所围成。(06-07)
所围成。(06-07)
提示:利用柱面或球面坐标均可以。
答案:
柱面: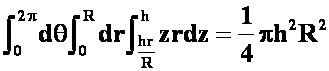
球面:
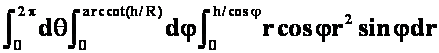 =
=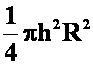
**例16计算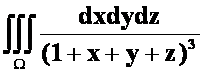 ,
,
![]() 所围四面体。
所围四面体。
提示:先一后二或先二后一均可。建议尽可能先一后二。
答案:
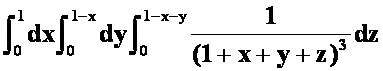
=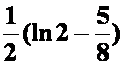
**例17求曲面![]() 被柱面
被柱面
![]()
所截下的部分的面积。
答案:
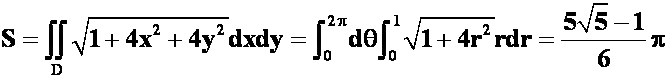 D为单位圆所围的平面区域。
D为单位圆所围的平面区域。
*例18 将下列积分化极坐标形式,并计算
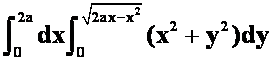
答案: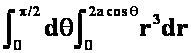 =
=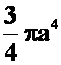
3、曲线积分与曲面积分;
*例19 ![]() ,
,![]() 顶点为(0,0),(3,0)和(3,2)的三角形的正向边界。(07-08)A
顶点为(0,0),(3,0)和(3,2)的三角形的正向边界。(07-08)A
提示:直接积分或用格林公式均可。
答案: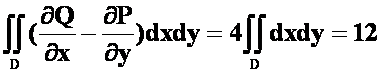 。
。
例20计算曲线积分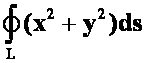 ,其中L是曲线
,其中L是曲线![]() 。(05-06)A
。(05-06)A
提示:技巧是将![]() 取代被积函数!
取代被积函数!
答案:![]()
例21计算曲线积分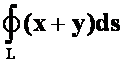 ,其中
,其中![]() 是直线
是直线![]() 与两坐标轴所围成的三角形的边界。(04-05b)
与两坐标轴所围成的三角形的边界。(04-05b)
答案: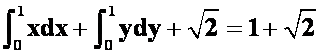
注意:下限必须小于上限。
例22
![]() 从
从![]() 到
到![]() (06-07)
(06-07)
提示:加B到A的直线段后用格林公式。
答案: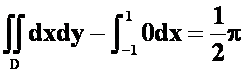
(D为单位圆的上半部分)
**例23: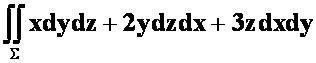 ,其中
,其中![]() 是上半球面
是上半球面![]() 的上侧。(05-06)A
的上侧。(05-06)A
提示:加底面(下侧)利用高斯公式。
答案: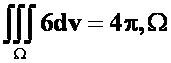 为上半球面。
为上半球面。
***例24:计算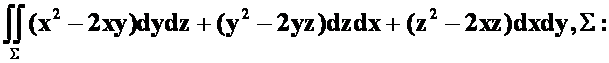 半球面
半球面![]() (
(![]() 的上侧,(08-09)
的上侧,(08-09)
提示:加底面z=a(下侧)利用高斯公式。
答案: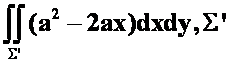 为
为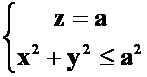 上侧。
上侧。
=![]()
**例25:利用高斯公式计算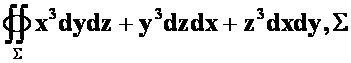 为球面
为球面![]() 的外侧。(06-07)
的外侧。(06-07)
错解:
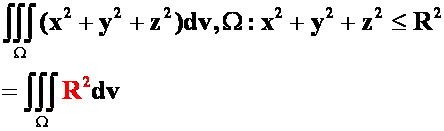
答案: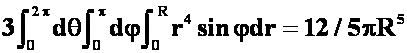
**例26: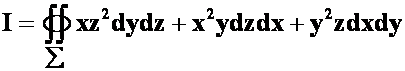
![]() 外侧(02-03)
外侧(02-03)
提示:典型的利用高斯公式。
答案: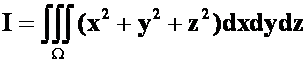 ,下面做法同上面例14。
,下面做法同上面例14。
**例27 求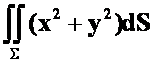 ,其中
,其中![]() 为锥面
为锥面
![]()
被平面z=0与z=3所截的部分。
注意:不要看做是二重积分。
答案: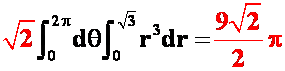
*例28计算曲线积分![]()
![]() (04-05)
(04-05)
提示:将![]() 代替被积函数。
代替被积函数。
答案:![]() 。
。
例29 计算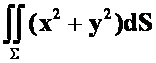 其中
其中![]() 为锥面
为锥面![]() 以及平面
以及平面![]() 围成的整个边界曲面。
围成的整个边界曲面。
答案: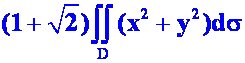
=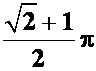
4.级数展开及其求和函数
例30将下列级数展开成幂级数,并指出收敛区间。
(1)![]()
(2)![]()
答案:(1)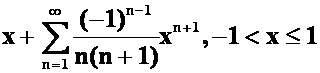
(2)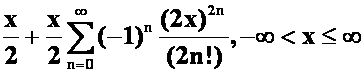
*例31:将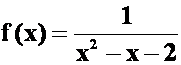 展成x的幂级数,并指出收敛区间。(06-07)A
展成x的幂级数,并指出收敛区间。(06-07)A
答案: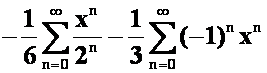
收敛区间:(-1,1)
**例32将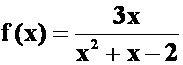 展开成
展开成![]() 的幂级数,并指明展开式成立的区间。
的幂级数,并指明展开式成立的区间。
提示:

答案:
成立区间:1<x<3
例33将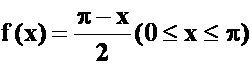 展成正弦级数。(07-08)
展成正弦级数。(07-08)
提示:对函数作奇延拓。
答案:
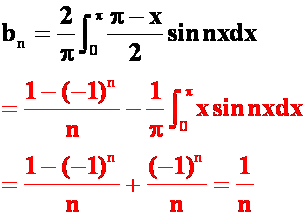
级数: 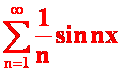 。
。
**例34求级数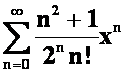 的和函数
的和函数
提示:利用指数函数展开式。
答案: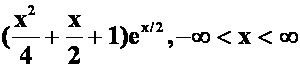
5.解微分方程。
*例35求![]() 的通解,。
的通解,。
提示:一阶线性: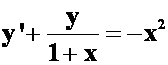
答案: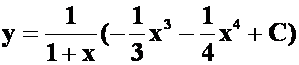
**例36设可导函数![]() 满足
满足
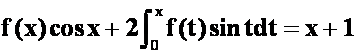 ,
,
求![]() (08-09)
(08-09)
提示:求导变有初值的微分方程
![]()
![]()
答案: ![]()
*例37求微分方程![]() 的通解。(04-05)B
的通解。(04-05)B
答案:![]() 。
。
*例38求微分方程![]() 的通解。
的通解。
提示:利用全微分方程
答案: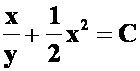
*例39求欧拉方程![]() 的通解。(05-06)A
的通解。(05-06)A
答案:令![]() 。方程变为
。方程变为
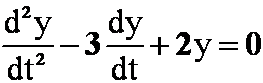
通解: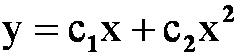
二、判断
*例40:判别下列级数的敛散性。
(1) (2)
(2)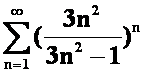
提示:(1)比值加重要极限。收敛。
(2)不满足收敛必要条件。发散。
*例41求幂级数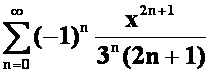 的收敛区间.(05-06)
的收敛区间.(05-06)
答案:收敛区间为![]() (注意边界)
(注意边界)
*例42判别下列级数是否收敛?若收敛,是条件收敛还是绝对收敛?
(1)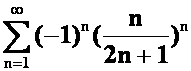 (2)
(2)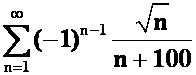 (07-08)
(07-08)
答案: (1)收敛;绝对收敛(比较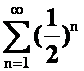 )。
)。
(2)收敛,条件收敛。证明{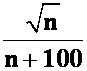 }(在n足够大时单调减可辅助函数:
}(在n足够大时单调减可辅助函数: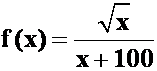 ,求导。
,求导。
**例43判断下列级数的敛散性
(1)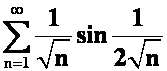 (2)
(2)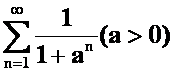
提示:(1)比较的极限形式(2)分情况讨论。
答案:(1)发散(2)![]() 时散,
时散,![]() 敛。
敛。
三、证明:
***例44设![]() ,(n=2,3,….)证明:当
,(n=2,3,….)证明:当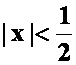 时,幂级数
时,幂级数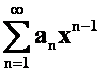 收敛,并求其和函数。(08-09)
收敛,并求其和函数。(08-09)
提示:易证![]() ,据阿贝尔判别法
,据阿贝尔判别法
答案:设n项和为![]() ,则用错项相减:
,则用错项相减:
![]()
两边同时取极限![]() 得和函数
得和函数
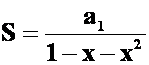
**例45设![]() 1。证明:若
1。证明:若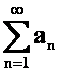 收敛,则
收敛,则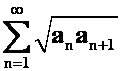 收敛。2,上述命题的逆命题是否成立?证明你的结论或给出反例。(06-07)
收敛。2,上述命题的逆命题是否成立?证明你的结论或给出反例。(06-07)
提示:利用不等式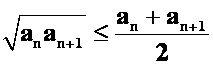
逆命题不成立,反例: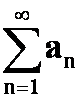 ,其中
,其中

*例46证明下列曲线积分与路径无关并计算:
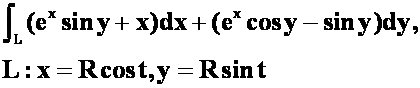
对应于![]() 从
从![]() 到
到![]() 的一段弧。(04-05)
的一段弧。(04-05)
提示:验证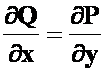 即可证明。
即可证明。
答案:0。
四、应用
例47一个半球状的雪堆,其体积融化的速度与半球面积![]() 成正比(比例常数为
成正比(比例常数为![]() ),假设在融化过程中雪堆始终保持半球状,已知半径为
),假设在融化过程中雪堆始终保持半球状,已知半径为![]() 的雪堆在开始融化的3小时内,融化了其体积的
的雪堆在开始融化的3小时内,融化了其体积的![]() ,问雪堆全部融化需要多少小时?(02-03)
,问雪堆全部融化需要多少小时?(02-03)
提示:![]()
列微分方程:
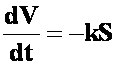
有: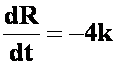 ,初值条件:
,初值条件:
![]()
![]()
答案: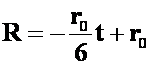 ,全部融化要6小时。
,全部融化要6小时。
**例48要造一个容积等于定值k的长方体无盖水池,应如何选择水池的尺寸,方可以使其表面积最小?
提示:设长宽高各为x,y,z
![]()
约束条件:xyz=k
用拉格朗日乘数法做。
答案:![]()
说明:后面标注的如(06-07)表示式取自06-07年度本校的试题。
打*号的表示难度,一个*表示较为简单的基本题,两个*表示难度中等,三个*表示较难。